
ISSN 0253-2778
CN 34-1054/N
Pool fires are one of the most commonly encountered flame types in fire disasters, and the accurate and detailed modeling of pool fires is beneficial for the hazard analysis and assessment of liquid-related fire accidents. The radiation model is known to be the critical component in the accurate simulation of various fire scenarios. Therefore, to develop a proper radiation model, an LES study of a large-scale methanol pool fire was performed in this work by coupling four different radiation models into the open-source fire simulation code FDS and solving the radiation intensity transport equation using the discrete ordinates method. The impact characteristics of different radiation models are evaluated in detail with the NIST experiments, where the comparative analysis was carried out. Regarding the temperature calculations, the WSGG (weighted-sum-of-gray-gases)-based radiation model and Cassol’s model performed better. In addition, all models predict pulsation frequencies well. However, regarding the prediction of the radiative heat fluxes, Cassol’s two models and the FDS default model outperformed the other models, which indicates that the database for obtaining the spectral information of each species and the method to determine the WSGG coefficient of mixed gases are significant factors for the successful prediction of flame radiation.
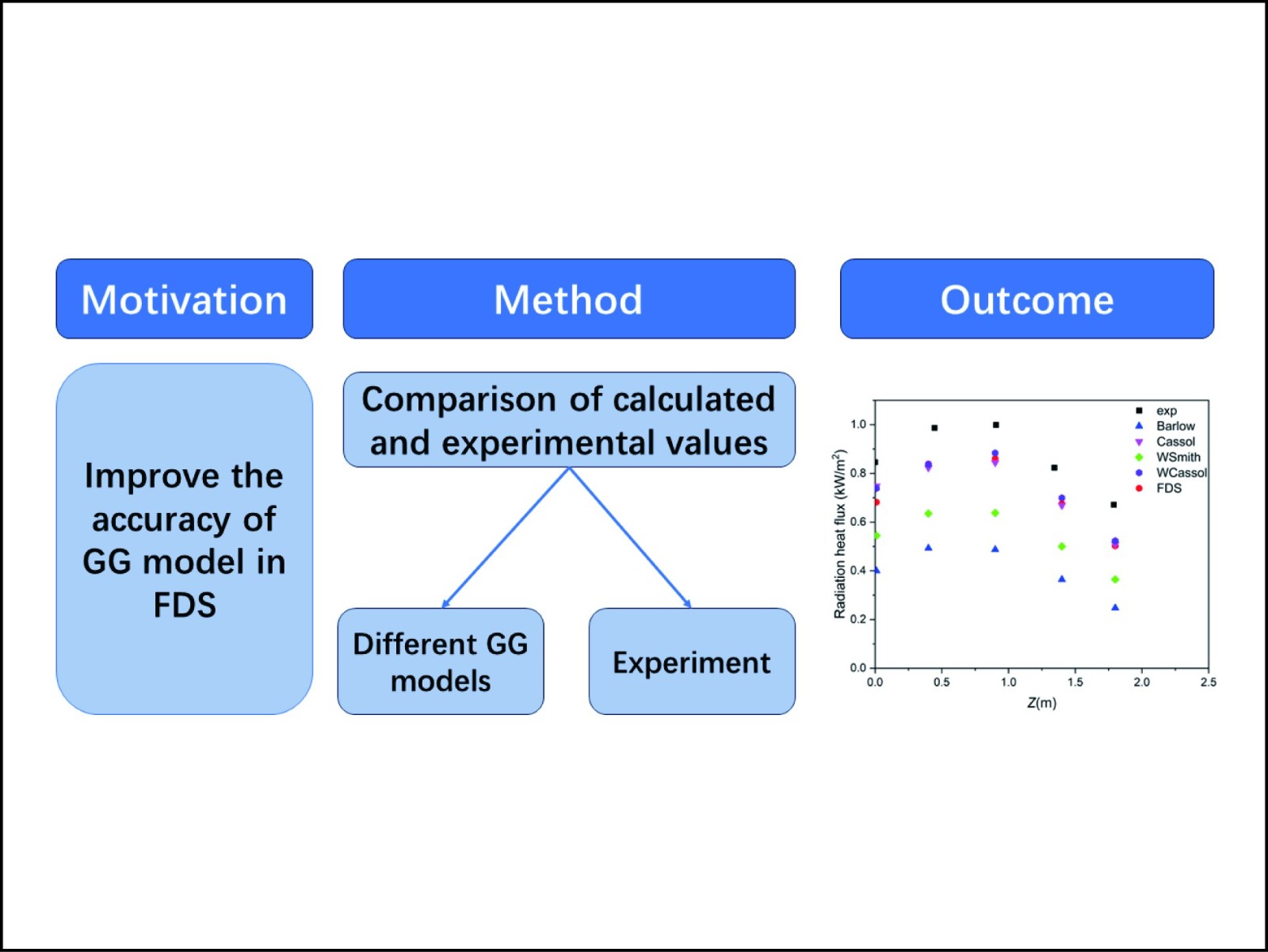
By comparing the improved models, the WCassol model and Cassol model have the best performance.
| [1] |
Abdolhamidzadeh B, Abbasi T, Rashtchian D, et al. Domino effect in process-industry accidents —An inventory of past events and identification of some patterns. Journal of Loss Prevention in the Process Industries, 2011, 24: 575–593. DOI: 10.1016/j.jlp.2010.06.013
|
| [2] |
Fang J, Wang J, Tu R, et al. Optical thickness of emissivity for pool fire radiation. International Journal of Thermal Sciences, 2018, 124: 338–343. DOI: 10.1016/j.ijthermalsci.2017.10.023
|
| [3] |
Sacadura J F. Radiative heat transfer in fire safety science. Journal of Quantitative Spectroscopy and Radiative Transfer, 2005, 93: 5–24. DOI: 10.1016/j.jqsrt.2004.08.011
|
| [4] |
Yao Y, Li Y Z, Ingason H, et al. Scale effect of mass loss rates for pool fires in an open environment and in tunnels with wind. Fire Safety Journal, 2019, 105: 41–50. DOI: 10.1016/j.firesaf.2019.02.004
|
| [5] |
Fernandes C S, Fraga G C, França F H R, et al. Radiative transfer calculations in fire simulations: An assessment of different gray gas models using the software FDS. Fire Safety Journal, 2021, 120: 103103. DOI: 10.1016/j.firesaf.2020.103103
|
| [6] |
Barlow R S, Karpetis A N, Frank J H, et al. Scalar profiles and NO formation in laminar opposed-flow partially premixed methane/air flames. Combustion and Flame, 2001, 127: 2102–2118. DOI: 10.1016/S0010-2180(01)00313-3
|
| [7] |
Cassol F, Brittes R, Centeno F R, et al. Evaluation of the gray gas model to compute radiative transfer in non-isothermal, non-homogeneous participating medium containing CO2, H2O, and soot. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2015, 37: 163–172. DOI: 10.1007/s40430-014-0168-5
|
| [8] |
Hostikka S, Mcgrattan K, Hamins A. Numerical modeling of pool fires using les and finite volume method for radiation. Fire Safety Science, 2003, 7: 383–394. DOI: 10.3801/IAFSS.FSS.7-383
|
| [9] |
Krishnamoorthy G, Borodai S, Rawat R, et al. Numerical modeling of radiative heat transfer in pool fire simulations. In: Proceedings of ASME 2005 International Mechanical Engineering Congress and Exposition. Orlando, Florida, USA: ASME, 2008: 327–337.
|
| [10] |
McGrattan K, McDermott R, Weinschenk C, et al. Fire Dynamics Simulator Users Guide, Sixth Edition, Special Publication (NIST SP). Gaithersburg, MD, USA: National Institute of Standards and Technology, 2013.
|
| [11] |
Sung K, Chen J, Bundy M, et al. The characteristics of a 1 m methanol pool fire. Fire Safety Journal, 2021, 120: 103121. DOI: 10.1016/j.firesaf.2020.103121
|
| [12] |
Grosshandler W L. Radcal: A Narrow-Band Model for Radiation Calculations in a Combustion Environment. Washington, DC: NIST, 2018.
|
| [13] |
Rothman L S, Gordon I E, Barber R J, et al. HITEMP, the high-temperature molecular spectroscopic database. Journal of Quantitative Spectroscopy and Radiative Transfer, 2010, 111: 2139–2150. DOI: 10.1016/j.jqsrt.2010.05.001
|
| [14] |
Smith T F, Shen Z F, Friedman J N. Evaluation of coefficients for the weighted sum of gray gases model. Journal of Heat Transfer, 1982, 104: 602–608. DOI: 10.1115/1.3245174
|
| [15] |
Cassol F, Brittes R, França F H R, et al. Application of the weighted-sum-of-gray-gases model for media composed of arbitrary concentrations of H2O, CO2 and soot. International Journal of Heat and Mass Transfer, 2014, 79: 796–806. DOI: 10.1016/j.ijheatmasstransfer.2014.08.032
|
| [16] |
Denison M K, Webb B W. The spectral-line weighted-sum-of-gray-gases model for H2O/CO2 mixtures. Journal of Heat Transfer, 1995, 117: 788–792. DOI: 10.1115/1.2822652
|
| [17] |
Johansson N, Ekholm M. Variation in results due to user effects in a simulation with FDS. Fire Technology, 2018, 54: 97–116. DOI: 10.1007/s10694-017-0674-y
|
| [18] |
McGrattan K, Hostikka S, McDermott R, et al. Fire Dynamics Simulator Technical Reference Guide Volume 1: Mathematical Model. Washington, DC: NIST, 2013.
|
| [19] |
Rehm R G, Baum H R. The equations of motion for thermally driven, buoyant flows. Journal of Research of the National Bureau of Standards, 1978, 83: 297. DOI: 10.6028/jres.083.019
|
| [20] |
Gottuk D T, White D A. Liquid fuel fires. In: Hurley M J, editor. SFPE Handbook of Fire Protection Engineering. New York: Springer, 2016: 2552−2590.
|
| [21] |
Fraga G C, Zannoni L, Centeno F R, et al. Evaluation of different gray gas formulations against line-by-line calculations in two- and three-dimensional configurations for participating media composed by CO2, H2O and soot. Fire Safety Journal, 2019, 108: 102843. DOI: 10.1016/j.firesaf.2019.102843
|
| [22] |
Dorigon L J, Duciak G, Brittes R, et al. WSGG correlations based on HITEMP2010 for computation of thermal radiation in non-isothermal, non-homogeneous H2O/CO2 mixtures. International Journal of Heat and Mass Transfer, 2013, 64: 863–873. DOI: 10.1016/j.ijheatmasstransfer.2013.05.010
|
| [23] |
Coelho F R, França F H R. WSGG correlations based on HITEMP2010 for gas mixtures of H2O and CO2 in high total pressure conditions. International Journal of Heat and Mass Transfer, 2018, 127: 105–114. DOI: 10.1016/j.ijheatmasstransfer.2018.07.075
|
| [24] |
Xu J, Chen R, Meng H. WSGG models for radiative heat transfer calculations in hydrogen and hydrogen-mixture flames at various pressures. International Journal of Hydrogen Energy, 2021, 46: 31452–31466. DOI: 10.1016/j.ijhydene.2021.07.040
|
| [25] |
da Fonseca R J C, Fraga G C, da Silva R B, et al. Application of the WSGG model to solve the radiative transfer in gaseous systems with nongray boundaries. Journal of Heat Transfer, 2018, 140: 052701. DOI: 10.1115/1.4038548
|
| [26] |
Hu L, Hu J, de Ris J L. Flame necking-in and instability characterization in small and medium pool fires with different lip heights. Combustion and Flame, 2015, 162: 1095–1103. DOI: 10.1016/j.combustflame.2014.10.001
|
| [27] |
Bejan A. Predicting the pool fire vortex shedding frequency. Journal of Heat Transfer, 1991, 113: 261–263. DOI: 10.1115/1.2910540
|
| [28] |
Chen X, Lu S, Wang X, et al. Pulsation behavior of pool fires in a confined compartment with a horizontal opening. Fire Technology, 2016, 52: 515–531. DOI: 10.1007/s10694-015-0484-z
|
| [29] |
Tieszen S R, O’Hern T J, Schefer R W, et al. Experimental study of the flow field in and around a one meter diameter methane fire. Combustion and Flame, 2002, 129: 378–391. DOI: 10.1016/S0010-2180(02)00352-8
|
| [30] |
Hottel H C, Sarofim A F. Radiative Transfer. New York: McGraw-hill Book Company, 1967.
|
| Entry | Catalyst |
T(°C) | Yieldb (g) | Activityb (106) | Mnc(104) | PDIc |
Branchd |
Tme(°C) |
| 1 | Ni1 | 0 | 2.65 | 3.18 | 38.2 | 1.8 | 7 | 128.2 |
| 2 | Ni1 | 30 | 5.43 | 6.51 | 33.6 | 2.1 | 21 | 118.0 |
| 3 | Ni1 | 60 | 2.52 | 3.02 | 21.9 | 2.0 | 40 | 114.4 |
| 4 | Ni1 | 90 | 2.01 | 2.41 | 16.6 | 2.1 | 41 | 114.0 |
| 5 | Ni2 | 0 | 2.35 | 2.82 | 37.6 | 1.8 | 15 | 120.2 |
| 6 | Ni2 | 30 | 4.11 | 4.93 | 29.7 | 1.9 | 26 | 117.0 |
| 7 | Ni2 | 60 | 2.76 | 3.31 | 17.3 | 2.1 | 46 | 113.6 |
| 8 | Ni2 | 90 | 0.90 | 1.08 | 14.8 | 2.1 | 61 | 80.9 |
| 9 | Ni3 | 0 | 1.10 | 1.32 | 16.2 | 2.3 | 36 | 115.1 |
| 10 | Ni3 | 30 | 1.94 | 2.33 | 12.8 | 2.6 | 51 | 106.1 |
| 11 | Ni3 | 60 | 0.80 | 0.96 | 11.9 | 3.1 | 72 | 69.1 |
| 12 | Ni3 | 90 | 0.02 | 0.02 | 11.5 | 3.2 | 94 | – |
| a 1 μmol of catalyst in CH2Cl2 (2 mL), [Al]/[Ni] = 500. Vn-heptane = 20 mL, tpolymerization = 10 min, Pethylene = 8 atm. b Activity is in units of 106 g·mol−1·h−1. c Determined by Gel Permeation Chromatography (GPC) in 1,2,4-trichlorobenzene at 150 °C. d Branches per 1000 carbons, determined by 1H NMR. e Determined by differential scanning calorimetry. | ||||||||