ISSN 0253-2778
CN 34-1054/N
Quantum discord has been proposed as a resource responsible for the exponential speedup in deterministic quantum computation with one pure qubit (DQC1). Investigation of the quantum discord generated in DQC1 is of significant importance from a fundamental perspective. However, in practical applications of DQC1, qubits generally interact with the environment. Thus, it is also important to investigate the discord when DQC1 is implemented in a noisy environment. We implement DQC1 on an electron spin resonance (ESR) architecture in such an environment and nonzero quantum discord is observed. Furthermore, we find that the values of discord correspond to the values of purity α and quantum Fisher information, which reflect the power of the algorithm. Our results provide further evidence for the role of discord as a resource in DQC1 and are beneficial for understanding the origin of the power of quantum algorithms.
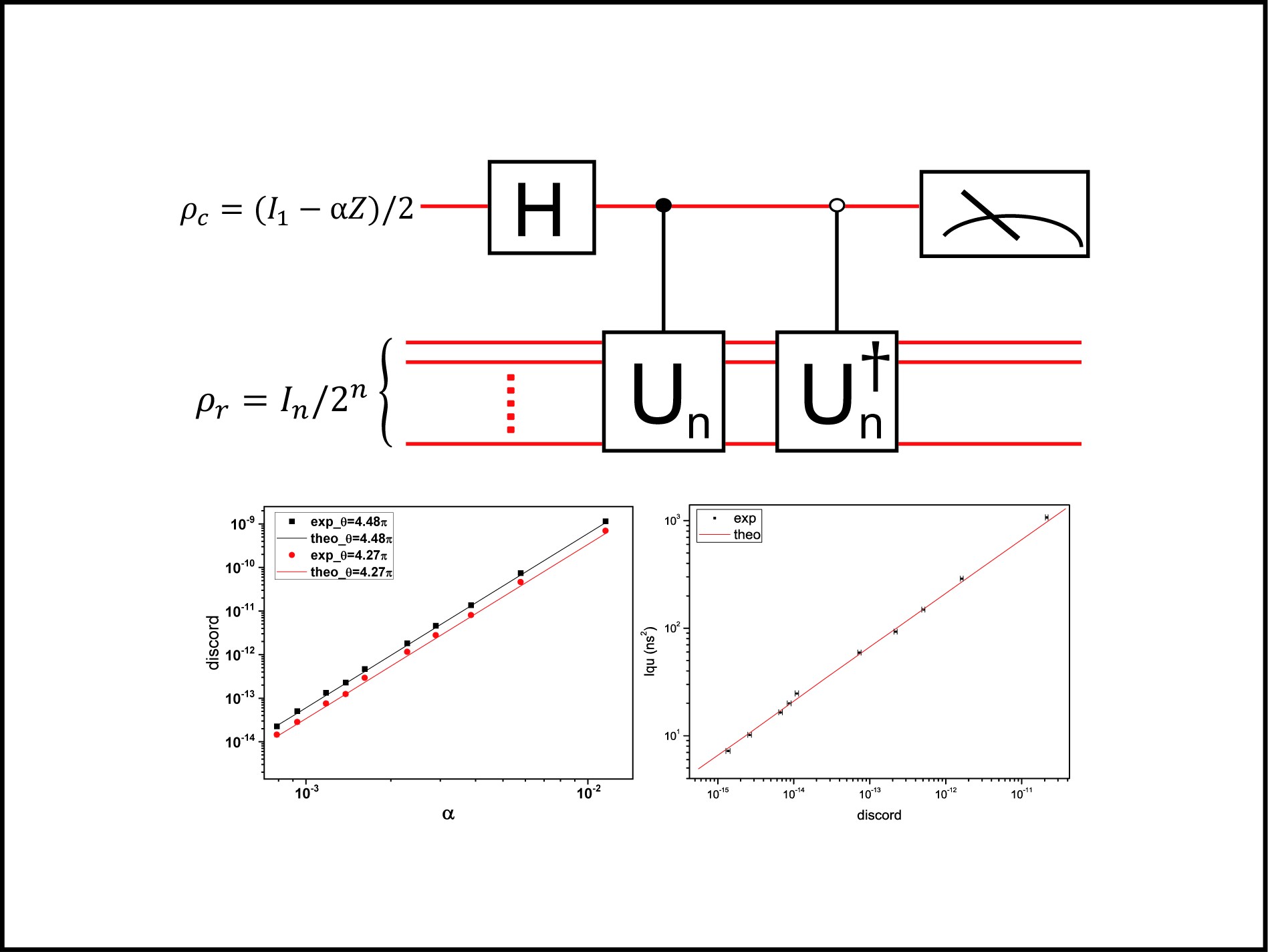
Quantum circuit of DQC1 algorithm and experimental results.
Figure
1.
DQC1 algorithm to estimate the normalized trace of
Figure
2.
(a) Continuous wave (
Figure
3.
Quantum discord generated for: (a)(c)
Figure
4.
(a) Experimentally detected quantum discord with varying temperature for
Figure
5.
Quantum Fisher information with quantum discord when implementing the DQC1 algorithm to estimate the hyperfine coupling
| [1] |
Shor P. Proceedings of the 35th Annual Symposium on the Foundations of Computer Science. Washington, D.C.: IEEE, 1994.
|
| [2] |
Galindo A, Martin-Delgado M A. Information and computation: Classical and quantum aspects. Reviews of Modern Physics, 2002, 74 (2): 347. DOI: 10.1103/RevModPhys.74.347
|
| [3] |
Goettems E I, Maciel T O, Soares-Pinto D O, et al. Promoting quantum correlations in deterministic quantum computation with a one-qubit model via postselection. Physical Review A, 2021, 103 (4): 042416. DOI: 10.1103/PhysRevA.103.042416
|
| [4] |
Göktaş O, Tham W K, Bonsma-Fisher K, et al. Benchmarking quantum processors with a single qubit. Quantum Information Processing, 2020, 19: 146. DOI: 10.1007/s11128-020-02642-4
|
| [5] |
Zhang K, Thompson J, Zhang X, et al. Modular quantum computation in a trapped ion system. Nature Communications, 2019, 10 (1): 1–6. DOI: 10.1038/s41467-018-07882-8
|
| [6] |
Krzyzanowska K, Copley-May M, Romain R, et al. Quantum-enhanced protocols with mixed states using cold atoms in dipole traps. Journal of Physics: Conference Series, 2017, 793 (1): 012015. DOI: 10.1088/1742-6596/793/1/012015
|
| [7] |
Pg S, Varikuti N D, Madhok V. Exponential speedup in measuring out-of-time-ordered correlators and gate fidelity with a single bit of quantum information. Physics Letters A, 2021, 397: 127257. DOI: 10.1016/j.physleta.2021.127257
|
| [8] |
Knill E, Laflamme R. Power of one bit of quantum information. Physical Review Letters, 1998, 81 (25): 5672. DOI: 10.1103/PhysRevLett.81.5672
|
| [9] |
Jozsa R, Linden N. On the role of entanglement in quantum-computational speed-up. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 2003, 459 (2036): 2011–2032. DOI: 10.1098/rspa.2002.1097
|
| [10] |
Horodecki R, Horodecki P, Horodecki M, et al. Quantum entanglement. Reviews of Modern Physics, 2009, 81 (2): 865–942. DOI: 10.1103/RevModPhys.81.865
|
| [11] |
Datta A, Flammia S T, Caves C M. Entanglement and the power of one qubit. Physical Review A, 2005, 72 (4): 042316. DOI: 10.1103/PhysRevA.72.042316
|
| [12] |
Boyer M, Brodutch A, Mor T. Entanglement and deterministic quantum computing with one qubit. Physical Review A, 2017, 95 (2): 022330. DOI: 10.1103/PhysRevA.95.022330
|
| [13] |
Bennett C H, DiVincenzo D P, Fuchs C A, et al. Quantum nonlocality without entanglement. Physical Review A, 1999, 59 (2): 1070. DOI: 10.1103/PhysRevA.59.1070
|
| [14] |
Modi K, Brodutch A, Cable H, et al. The classical-quantum boundary for correlations: Discord and related measures. Reviews of Modern Physics, 2012, 84 (4): 1655. DOI: 10.1103/RevModPhys.84.1655
|
| [15] |
Hu M L, Hu X, Wang J, et al. Quantum coherence and geometric quantum discord. Physics Reports, 2018, 762: 1–100. DOI: 10.1016/j.physrep.2018.07.004
|
| [16] |
Bera A, Das T, Sadhukhan D, et al. Quantum discord and its allies: A review of recent progress. Reports on Progress in Physics, 2017, 81 (2): 024001. DOI: 10.1088/1361-6633/aa872f
|
| [17] |
Datta A, Shaji A, Caves C M. Quantum discord and the power of one qubit. Physical Review Letters, 2008, 100 (5): 050502. DOI: 10.1103/PhysRevLett.100.050502
|
| [18] |
Madsen L S, Berni A, Lassen M, et al. Experimental investigation of the evolution of Gaussian quantum discord in an open system. Physical Review Letters, 2012, 109 (3): 030402. DOI: 10.1103/PhysRevLett.109.030402
|
| [19] |
Radhakrishnan C, Lauriere M, Byrnes T. Multipartite generalization of quantum discord. Physical Review Letters, 2020, 124 (11): 110401. DOI: 10.1103/PhysRevLett.124.110401
|
| [20] |
Hunt M A, Lerner I V, Yurkevich I V, et al. How to observe and quantify quantum-discord states via correlations. Physical Review A, 2019, 100 (2): 022321. DOI: 10.1103/PhysRevA.100.022321
|
| [21] |
Faba J, Martín V, Robledo L. Two-orbital quantum discord in fermion systems. Physical Review A, 2021, 103 (3): 032426. DOI: 10.1103/PhysRevA.103.032426
|
| [22] |
Gu M, Chrzanowski H M, Assad S M, et al. Observing the operational significance of discord consumption. Nature Physics, 2012, 8 (9): 671–675. DOI: 10.1038/nphys2376
|
| [23] |
Dakić B, Lipp Y O, Ma X, et al. Quantum discord as resource for remote state preparation. Nature Physics, 2012, 8 (9): 666–670. DOI: 10.1038/nphys2377
|
| [24] |
Lanyon B P, Barbieri M, Almeida M P, et al. Experimental quantum computing without entanglement. Physical Review Letters, 2008, 101 (20): 200501. DOI: 10.1103/PhysRevLett.101.200501
|
| [25] |
Passante G, Moussa O, Trottier D A, et al. Experimental detection of nonclassical correlations in mixed-state quantum computation. Physical Review A, 2011, 84 (4): 044302. DOI: 10.1103/PhysRevA.84.044302
|
| [26] |
Hor-Meyll M, Tasca D S, Walborn S P, et al. Deterministic quantum computation with one photonic qubit. Physical Review A, 2015, 92 (1): 012337. DOI: 10.1103/PhysRevA.92.012337
|
| [27] |
Wang W, Han J, Yadin B, et al. Witnessing quantum resource conversion within deterministic quantum computation using one pure superconducting qubit. Physical Review Letters, 2019, 123 (22): 220501. DOI: 10.1103/PhysRevLett.123.220501
|
| [28] |
Ferraro A, Aolita L, Cavalcanti D, et al. Almost all quantum states have nonclassical correlations. Physical Review A, 2010, 81 (5): 052318. DOI: 10.1103/PhysRevA.81.052318
|
| [29] |
Cable H, Gu M, Modi K. Power of one bit of quantum information in quantum metrology. Physical Review A, 2016, 93 (4): 040304. DOI: 10.1103/PhysRevA.93.040304
|
| [30] |
Dorner R, Clark S R, Heaney L, et al. Extracting quantum work statistics and fluctuation theorems by single-qubit interferometry. Physical Review Letters, 2013, 110 (23): 230601. DOI: 10.1103/PhysRevLett.110.230601
|
| [31] |
Ryan C A, Emerson J, Poulin D, et al. Characterization of complex quantum dynamics with a scalable NMR information processor. Physical Review Letters, 2005, 95 (25): 250502. DOI: 10.1103/PhysRevLett.95.250502
|
| [32] |
Passante G, Moussa O, Ryan C A, et al. Experimental approximation of the Jones polynomial with one quantum bit. Physical Review Letters, 2009, 103 (25): 250501. DOI: 10.1103/PhysRevLett.103.250501
|
| [33] |
Helstrom C W. Minimum mean-squared error of estimates in quantum statistics. Physics Letters A, 1967, 25 (2): 101–102. DOI: 10.1016/0375-9601(67)90366-0
|
| [34] |
Braunstein S L, Caves C M. Statistical distance and the geometry of quantum states. Physical Review Letters, 1994, 72 (22): 3439. DOI: 10.1103/PhysRevLett.72.3439
|
| [35] |
Barndorff-Nielsen O E, Gill R D. Fisher information in quantum statistics. Journal of Physics A: Mathematical and General, 2000, 33 (24): 4481. DOI: 10.1088/0305-4470/33/24/306
|
| [36] |
Weeks R A. Paramagnetic resonance of lattice defects in irradiated quartz. Journal of Applied Physics, 1956, 27 (11): 1376–1381. DOI: 10.1063/1.1722267
|
| [37] |
Weeks R A, Nelson C M. Trapped electrons in irradiated quartz and silica: II, electron spin resonance. Journal of the American Ceramic Society, 1960, 43 (8): 399–404. DOI: 10.1111/j.1151-2916.1960.tb13682.x
|
| [38] |
Weeks R A. Paramagnetic spectra of E2' centers in crystalline quartz. Physical Review, 1963, 130 (2): 570. DOI: 10.1103/PhysRev.130.570
|
| [39] |
Rudra J K, Fowler W B, Feigl F J. Model for the E2' center in alpha quartz. Physical Review Letters, 1985, 55 (23): 2614. DOI: 10.1103/PhysRevLett.55.2614
|
| [40] |
Perlson B D, Weil J A. Electron paramagnetic resonance studies of the E' centers in alpha-quartz. Canadian Journal of Physics, 2008, 86 (7): 871–881. DOI: 10.1139/p08-034
|
| [41] |
Feng P, Wang Y, Rong X, et al. Characterization of the electronic structure of E2' defect in quartz by pulsed EPR spectroscopy. Physics Letters A, 2012, 376 (32): 2195–2199. DOI: 10.1016/j.physleta.2012.05.029
|
| [42] |
Vandersypen L M K, Chuang I L. NMR techniques for quantum control and computation. Reviews of Modern Physics, 2005, 76 (4): 1037. DOI: 10.1103/RevModPhys.76.1037
|
| [43] |
Braunstein S L, Caves C M, Milburn G J. Generalized uncertainty relations: Theory, examples, and Lorentz invariance. Annals of Physics, 1996, 247 (1): 135–173. DOI: 10.1006/aphy.1996.0040
|