ISSN 0253-2778
CN 34-1054/N
The physics-informed neural network (PINN) is an emerging approach for efficiently solving partial differential equations (PDEs) using neural networks. The physics-informed convolutional neural network (PICNN), a variant of PINN enhanced by convolutional neural networks (CNNs), has achieved better results on a series of PDEs since the parameter-sharing property of CNNs is effective in learning spatial dependencies. However, applying existing PICNN-based methods to solve Navier–Stokes equations can generate oscillating predictions, which are inconsistent with the laws of physics and the conservation properties. To address this issue, we propose a novel method that combines PICNN with the finite volume method to obtain physically plausible and conservative solutions to Navier–Stokes equations. We derive the second-order upwind difference scheme of Navier–Stokes equations using the finite volume method. Then we use the derived scheme to calculate the partial derivatives and construct the physics-informed loss function. The proposed method is assessed by experiments on steady-state Navier–Stokes equations under different scenarios, including convective heat transfer and lid-driven cavity flow. The experimental results demonstrate that our method can effectively improve the plausibility and accuracy of the predicted solutions from PICNN.
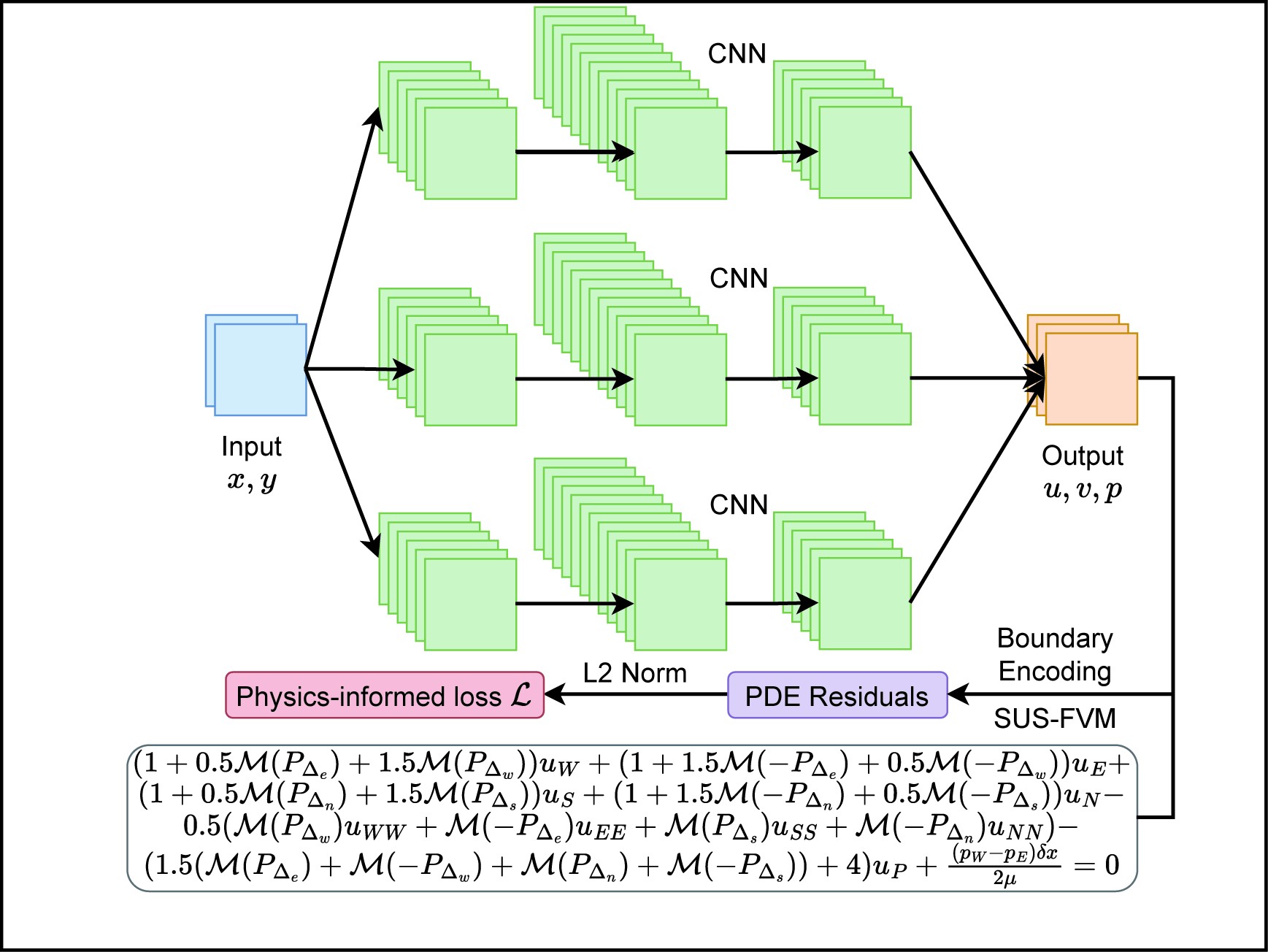
Schematic illustration for solving the Navier–Stokes equations using physics-informed CNNs.
| [1] |
Wang N, Chang H, Zhang D, et al. Efficient well placement optimization based on theory-guided convolutional neural network. Journal of Petroleum Science and Engineering, 2022, 208: 109545. DOI: 10.1016/j.petrol.2021.109545
|
| [2] |
Raissi M, Perdikaris P, Karniadakis G E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational Physics, 2019, 378: 686–707. DOI: 10.1016/j.jcp.2018.10.045
|
| [3] |
Wang N, Chang H, Zhang D. Efficient uncertainty quantification and data assimilation via theory-guided convolutional neural network. SPE Journal, 2021, 26 (06): 4128–4156. DOI: 10.2118/203904-PA
|
| [4] |
Meng C, Seo S, Cao D, et al. When physics meets machine learning: A survey of physics-informed machine learning. arXiv: 2203.16797, 2022.
|
| [5] |
Baydin A G, Pearlmutter B A, Radul A A, et al. Automatic differentiation in machine learning: A survey. Journal of Marchine Learning Research, 2017, 18 (1): 5595–5637. DOI: 10.5555/3122009.3242010
|
| [6] |
Geneva N, Zabaras N. Modeling the dynamics of PDE systems with physics-constrained deep auto-regressive networks. Journal of Computational Physics, 2020, 403: 109056. DOI: 10.1016/j.jcp.2019.109056
|
| [7] |
Winovich N, Ramani K, Lin G. ConvPDE-UQ: Convolutional neural networks with quantified uncertainty for heterogeneous elliptic partial differential equations on varied domains. Journal of Computational Physics, 2019, 394: 263–279. DOI: 10.1016/j.jcp.2019.05.026
|
| [8] |
Ren P, Rao C, Liu Y, et al. Physics-informed deep super-resolution for spatiotemporal data. arXiv: 2208.01462, 2022
|
| [9] |
Gao H, Sun L, Wang J X. PhyGeoNet: Physics-informed geometry-adaptive convolutional neural networks for solving parameterized steady-state PDEs on irregular domain. Journal of Computational Physics, 2021, 428: 110079. DOI: 10.1016/j.jcp.2020.110079
|
| [10] |
Ren P, Rao C, Liu Y, et al. PhyCRNet: Physics-informed convolutional-recurrent network for solving spatiotemporal PDEs. Computer Methods in Applied Mechanics and Engineering, 2022, 389: 114399. DOI: 10.1016/j.cma.2021.114399
|
| [11] |
Jaluria Y, Torrance K E. Computational Heat Transfer. Heidelberg: Springer Berlin, 2017
|
| [12] |
Zhang R, Liu Y, Sun H. Physics-guided convolutional neural network (PhyCNN) for data-driven seismic response modeling. Engineering Structures, 2020, 215: 110704. DOI: 10.1016/j.engstruct.2020.110704
|
| [13] |
Sun L, Wang J X. Physics-constrained Bayesian neural network for fluid flow reconstruction with sparse and noisy data. Theoretical and Applied Mechanics Letters, 2020, 10: 161–169. DOI: 10.1016/j.taml.2020.01.031
|
| [14] |
Wang Y, Sun H, Sun G. DSP-PIGAN: A precision-consistency machine learning algorithm for solving partial differential equations. In: 2021 13th International Conference on Machine Learning and Computing. New York: ACM, 2021: 21–26.
|
| [15] |
Zhu Y, Zabaras N, Koutsourelakis P S, et al. Physics-constrained deep learning for high-dimensional surrogate modeling and uncertainty quantification without labeled data. Journal of Computational Physics, 2019, 394: 56–81. DOI: 10.1016/j.jcp.2019.05.024
|
| [16] |
Sun L, Gao H, Pan S, et al. Surrogate modeling for fluid flows based on physics-constrained deep learning without simulation data. Computer Methods in Applied Mechanics and Engineering, 2020, 361: 112732. DOI: 10.1016/j.cma.2019.112732
|
| [17] |
Yang Y, Perdikaris P. Adversarial uncertainty quantification in physics-informed neural networks. Journal of Computational Physics, 2019, 394: 136–152. DOI: 10.1016/j.jcp.2019.05.027
|
| [18] |
Meng X, Li Z, Zhang D, et al. PPINN: Parareal physics-informed neural network for time-dependent PDEs. Computer Methods in Applied Mechanics and Engineering, 2020, 370: 113250. DOI: 10.1016/j.cma.2020.113250
|
| [19] |
Pang G, Lu L, Karniadakis G E. fPINNs: Fractional physics-informed neural networks. SIAM Journal on Scientific Computing, 2019, 41 (4): A2603–A2626. DOI: 10.1137/18M1229845
|
| [20] |
Kharazmi E, Zhang Z, Karniadakis G E. Variational physics-informed neural networks for solving partial differential equations. arXiv: 1912.00873, 2019.
|
| [21] |
Yang L, Meng X, Karniadakis G E. B-PINNs: Bayesian physics-informed neural networks for forward and inverse PDE problems with noisy data. Journal of Computational Physics, 2021, 425: 109913. DOI: 10.1016/j.jcp.2020.109913
|
| [22] |
Rao C, Liu Y. Three-dimensional convolutional neural network (3D-CNN) for heterogeneous material homogenization. Computational Materials Science, 2020, 184: 109850. DOI: 10.1016/j.commatsci.2020.109850
|
| [23] |
Zhu Y, Zabaras N. Bayesian deep convolutional encoder-decoder networks for surrogate modeling and uncertainty quantification. Journal of Computational Physics, 2018, 366: 415–447. DOI: 10.1016/j.jcp.2018.04.018
|
| [24] |
Kim B, Azevedo V C, Thuerey N, et al. Deep fluids: A generative network for parameterized fluid simulations. Computer Graphics Forum, 2019, 38: 59–70.
|
| [25] |
Sharma R, Farimani A B, Gomes J, et al. Weakly-supervised deep learning of heat transport via physics informed loss. arXiv: 1807.11374, 2018.
|
| [26] |
Fukui K I, Tanaka J, Tomita T, et al. Physics-guided neural network with model discrepancy based on upper troposphere wind prediction. In: 2019 18th IEEE International Conference on Machine Learning and Applications (ICMLA). Boca Raton, USA: IEEE, 2019: 414–419.
|
| [27] |
Subramaniam A, Wong M L, Borker R D, et al. Turbulence enrichment using physics-informed generative adversarial networks. arXiv: 2003.01907, 2020.
|
| [28] |
Mohan A T, Lubbers N, Livescu D, et al. Embedding hard physical constraints in neural network coarse-graining of 3D turbulence. arXiv: 2002.00021, 2020.
|
| [29] |
Bar-Sinai Y, Hoyer S, Hickey J, et al. Learning data-driven discretizations for partial differential equations. Proceedings of the National Academy of Sciences of the United States of America, 2019, 116: 15344–15349. DOI: 10.1073/pnas.1814058116
|
| [30] |
Tao W Q. Numerical Heat Transfer, second edtion. Xi’an, China: Xi’an Jiaotong University Press, 2001.
|
| [31] |
Guo L, Ye S, Han J, et al. SSR-VFD: Spatial super-resolution for vector field data analysis and visualization. In: 2020 IEEE Pacific Visualization Symposium (PacificVis). Tianjin, China: IEEE, 2020: 71–80.
|
| [32] |
Lu L, Meng X, Mao Z, et al. DeepXDE: A deep learning library for solving differential equations. SIAM Review, 2021, 63: 208–228. DOI: 10.1137/19M1274067
|
| [33] |
Wu C, Zhu M, Tan Q, et al. A comprehensive study of non-adaptive and residual-based adaptive sampling for physics-informed neural networks. Computer Methods in Applied Mechanics and Engineering, 2023, 403: 115671. DOI: 10.1016/j.cma.2022.115671
|
| [34] |
Yu J, Lu L, Meng X, et al. Gradient-enhanced physics-informed neural networks for forward and inverse PDE problems. Computer Methods in Applied Mechanics and Engineering, 2022, 393: 114823. DOI: 10.1016/j.cma.2022.114823
|
| [35] |
Wang S, Wang H, Perdikaris P. On the eigenvector bias of Fourier feature networks: From regression to solving multi-scale PDEs with physics-informed neural networks. Computer Methods in Applied Mechanics and Engineering, 2021, 384: 113938. DOI: 10.1016/j.cma.2021.113938
|
| CD-FVM | SUS-FVM | ||
| Re=30 | Pressure | 0.0478 | 0.0675 |
| Velocity | 0.0318 | 0.0393 | |
| Re=150 | Pressure | 0.0456 | 0.0855 |
| Velocity | 0.0404 | 0.0389 | |
| Re=300 | Pressure | 0.0967 | 0.0839 |
| Velocity | 0.1280 | 0.0486 |
| CD-FVM | CD-FDM | SUS-FVM | SUS-FDM | ||
| Re=30 | Pressure | 0.0478 | 0.1392 | 0.0675 | 0.7760 |
| Velocity | 0.0318 | 0.1078 | 0.0393 | 0.3281 | |
| Re=300 | Pressure | 0.0967 | – | 0.0839 | – |
| Velocity | 0.1280 | – | 0.0486 | – | |
| Dash “–” means divergence and error cannot be calculated. | |||||
| DeepXDE-s | DeepXDE-l | SUS-FVM | ||
| Re=30 | Pressure | 0.4420 | 0.3588 | 0.0675 |
| Velocity | 0.2233 | 0.1715 | 0.0393 | |
| Re=150 | Pressure | 0.9956 | 0.5955 | 0.0855 |
| Velocity | 0.6086 | 0.4062 | 0.0389 | |
| Re=300 | Pressure | 1.5442 | 0.6548 | 0.0839 |
| Velocity | 0.7859 | 0.4522 | 0.0486 |
| CD-FVM | SUS-FVM | |
| Data1: k=10 | 0.0023 | 0.0027 |
| Data2: k=1 | 0.0196 | 0.0042 |
| Data3: k=0.5 | 0.0338 | 0.0076 |
| Data4: k=0.1 | 0.0922 | 0.0293 |
| Re=500, ρ=1, Cp=1000 | ||
| CD-FVM | SUS-FVM | ||
| Re=100 | pressure | 0.4277 | 0.3986 |
| velocity | 0.1082 | 0.1074 | |
| Re=500 | pressure | 0.2873 | 0.2125 |
| velocity | 0.1644 | 0.1317 | |
| Re=1000 | pressure | 0.3737 | 0.3395 |
| velocity | 0.2936 | 0.2768 |