ISSN 0253-2778
CN 34-1054/N
Exploring millimeter wave radar data as complementary to RGB images for ameliorating 3D object detection has become an emerging trend for autonomous driving systems. However, existing radar-camera fusion methods are highly dependent on the prior camera detection results, rendering the overall performance unsatisfactory. In this paper, we propose a bidirectional fusion scheme in the bird-eye view (BEV-radar), which is independent of prior camera detection results. Leveraging features from both modalities, our method designs a bidirectional attention-based fusion strategy. Specifically, following BEV-based 3D detection methods, our method engages a bidirectional transformer to embed information from both modalities and enforces the local spatial relationship according to subsequent convolution blocks. After embedding the features, the BEV features are decoded in the 3D object prediction head. We evaluate our method on the nuScenes dataset, achieving 48.2 mAP and 57.6 NDS. The result shows considerable improvements compared to the camera-only baseline, especially in terms of velocity prediction. The code is available at https://github.com/Etah0409/BEV-Radar.
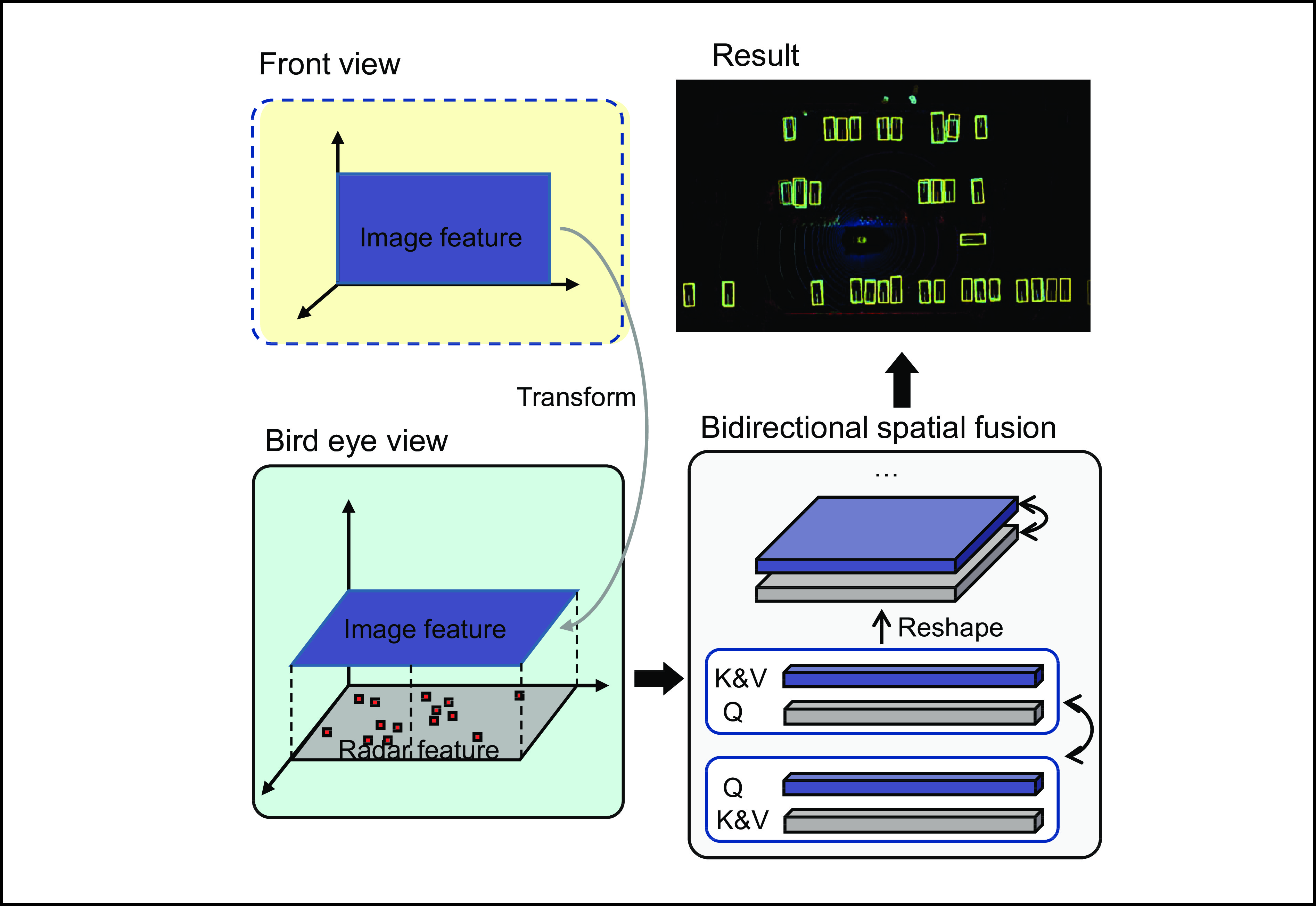
BEV-radar simplifies 3D object detection by aligning camera and radar features in a bird-eye view (BEV) perspective, enhancing fusion through a bidirectional query-based transformer approach for complementary information exchange.
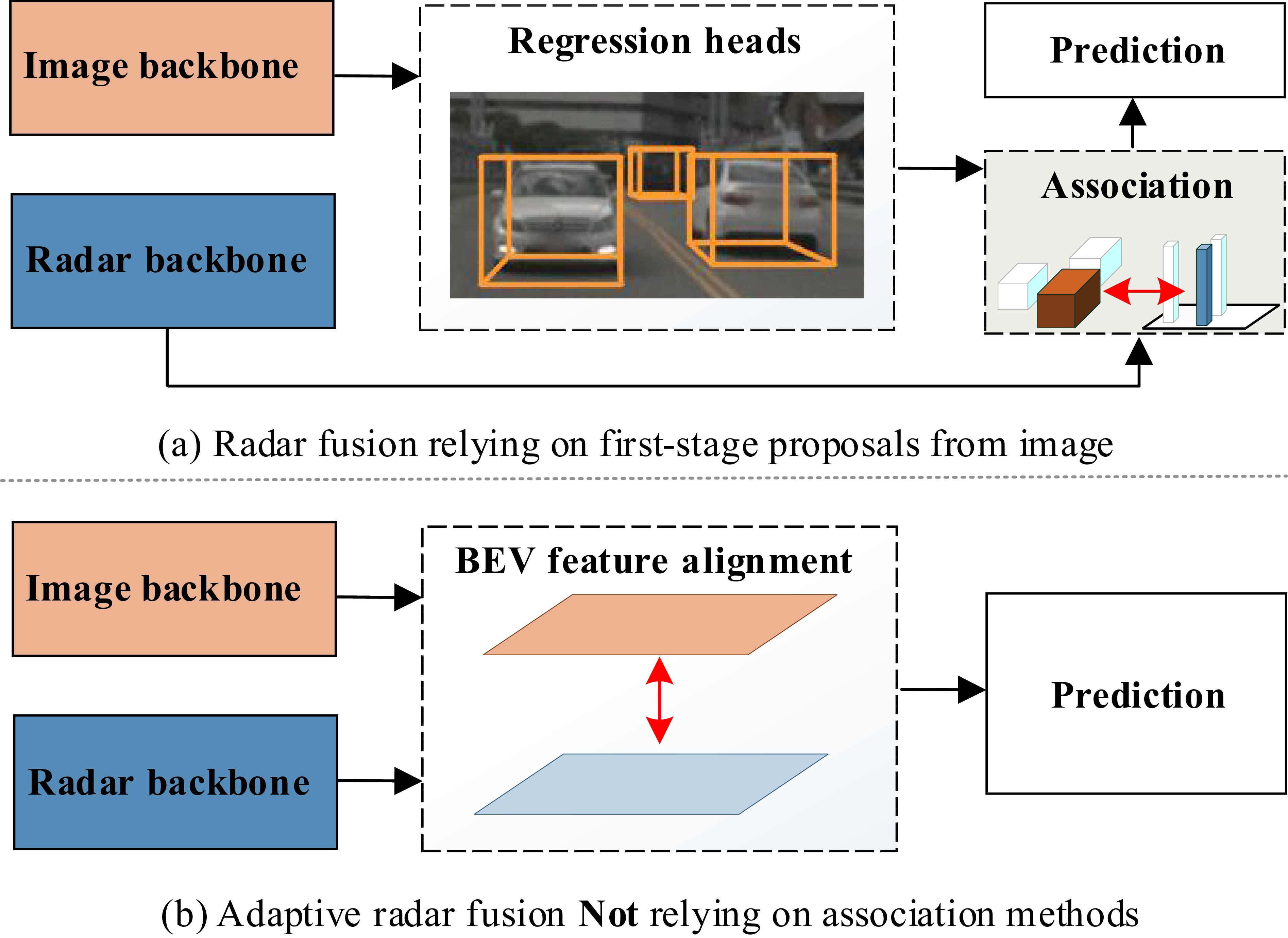
Figure 1. Comparison between the two alignment methods. (a) Radar fusion methods relying on the first stage proposals: after generating the initial proposals, association methods to their corresponding radar regions is necessary, leading to ignoring of objects which are not detected in the first stage. (b) Our adaptive radar fusion view: instead of aligning proposals from the first stage, features are directly aligned in BEV, thus prediction is guided by multi-modality features.
Figure 2. Overall architecture of framework. Our model is constructed on separate backbones to extract the image BEV features and the radar BEV features. Our BSF (bidirectional spatial fusion) blocks consist of several blocks sequentially: First, a shared bidirectional cross-attention for communicating both modalities. Spatial alignment is followed to localize the radar and camera BEV features. After all blocks, both outputs will be sent in a deconvolution module to descend the channel.
Figure 3. In the first row, base prediction and fusion prediction separately represent the camera-only model and the radar-fusion model on BEV. The ground truth is plotted as blue boxes and the prediction boxes are plotted as yellow boxes, with lighter colors indicating higher confidence scores. The bottom row shows a visualization of the camera views for this frame, with the corresponding regions of interest marked by dashed boxes of the same color.
Figure 4. Qualitative analysis of detection results. 3D bounding box predictions are projected onto images from six different views and BEV respectively. Boxes from different categories are marked with different colors and without ground truth. For BEV visualization, yellow means predicted boxes and blue ones are ground-truth, while LiDAR points are visualized as background.
| [1] |
Vora S, Lang A H, Helou B, et al. PointPainting: Sequential fusion for 3D object detection. In: 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Seattle, USA: IEEE, 2020: 4603–4611.
|
| [2] |
Long Y, Morris D, Liu X, et al. Radar-camera pixel depth association for depth completion. In: 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Nashville, USA: IEEE, 2021: 12502–12511.
|
| [3] |
Nobis F, Geisslinger M, Weber M, et al. A deep learning-based radar and camera sensor fusion architecture for object detection. In: 2019 Sensor Data Fusion: Trends, Solutions, Applications (SDF). Bonn, Germany: IEEE, 2019: 1–7.
|
| [4] |
Liu Z, Tang H, Amini A, et al. BEVFusion: Multi-task multi-sensor fusion with unified bird’s-eye view representation. arXiv: 2205.13542, 2022.
|
| [5] |
Huang J, Huang G, Zhu Z, et al. BEVDet: High-performance multi-camera 3D object detection in bird-eye-view. arXiv: 2112.11790, 2021.
|
| [6] |
Xu B, Chen Z. Multi-level fusion based 3D object detection from monocular images. In: 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, USA: IEEE, 2018: 2345–2353.
|
| [7] |
Kundu A, Li Y, Rehg J M. 3D-RCNN: Instance-level 3D object reconstruction via render-and-compare. In: 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, USA: IEEE, 2018: 3559–3568.
|
| [8] |
You Y, Wang Y, Chao W L, et al. Pseudo-LiDAR++: Accurate depth for 3D object detection in autonomous driving. In: Eighth International Conference on Learning Representations, 2020.
|
| [9] |
Wang Y, Chao W L, Garg D, et al. Pseudo-LiDAR from visual depth estimation: Bridging the gap in 3D object detection for autonomous driving. In: 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Long Beach, USA: IEEE, 2020: 8437–8445.
|
| [10] |
Roddick T, Kendall A, Cipolla R. Orthographic feature transform for monocular 3D object detection. arXiv: 1811.08188, 2018.
|
| [11] |
Wang T, Zhu X, Pang J, et al. FCOS3D: Fully convolutional one-stage monocular 3D object detection. In: 2021 IEEE/CVF International Conference on Computer Vision Workshops (ICCVW). Montreal, Canada: IEEE, 2021: 913–922.
|
| [12] |
Li Z, Wang W, Li H, et al. BEVFormer: Learning bird’s-eye-view representation from multi-camera images via spatiotemporal transformers. In: Avidan S, Brostow G, Cissé M, et al. Editors. Computer Vision–ECCV 2022. Cham: Springer, 2022: 1–18.
|
| [13] |
Wang Y, Guizilini V, Zhang T, et al. DETR3D: 3D object detection from multi-view images via 3D-to-2D queries. In: 5th Conference on Robot Learning(CoRL 2021). London, UK: CoRL, 2021: 1–12.
|
| [14] |
Chen X, Ma H, Wan J, et al. Multi-view 3D object detection network for autonomous driving. In: 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Honolulu, USA: IEEE, 2017: 6526–6534.
|
| [15] |
Qi C R, Liu W, Wu C, et al. Frustum PointNets for 3D object detection from RGB-D data. In: 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, USA: IEEE, 2018: 918–927.
|
| [16] |
Qian K, Zhu S, Zhang X, et al. Robust multimodal vehicle detection in foggy weather using complementary LiDAR and radar signals. In: 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Nashville, USA: IEEE, 2021: 444–453.
|
| [17] |
Chadwick S, Maddern W, Newman P. Distant vehicle detection using radar and vision. In: 2019 International Conference on Robotics and Automation (ICRA). Montreal, Canada: IEEE, 2019: 8311–8317.
|
| [18] |
Cheng Y, Xu H, Liu Y. Robust small object detection on the water surface through fusion of camera and millimeter wave radar. In: 2021 IEEE/CVF International Conference on Computer Vision (ICCV). Montreal, Canada: IEEE, 2022: 15243–15252.
|
| [19] |
Bai X, Hu Z, Zhu X, et al. TransFusion: robust LiDAR-camera fusion for 3D object detection with transformers. In: 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). New Orleans, USA: IEEE, 2022: 1080–1089.
|
| [20] |
Liu Z, Lin Y, Cao Y, et al. Swin transformer: Hierarchical vision transformer using shifted windows. In: 2021 IEEE/CVF International Conference on Computer Vision (ICCV). Montreal, Canada: IEEE, 2021: 9992–10002.
|
| [21] |
Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need. In: Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach, USA: Curran Associates Inc., 2017: 6000–6010.
|
| [22] |
Carion N, Massa F, Synnaeve G, et al. End-to-end object detection with transformers. In: Vedaldi A, Bischof H, Brox T, et al. editors. Computer Vision–ECCV 2020. Cham: Springer, 2020: 213–229.
|
| [23] |
Zhang R, Qiu H, Wang T, et al. MonoDETR: Depth-guided transformer for monocular 3D object detection. arXiv: 2203.13310, 2022.
|
| [24] |
Zhu X, Su W, Lu L, et al. Deformable DETR: Deformable transformers for end-to-end object detection. arXiv: 2010.04159, 2020.
|
| [25] |
Lang A H, Vora S, Caesar H, et al. PointPillars: fast encoders for object detection from point clouds. In: 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Long Beach, USA: IEEE, 2019: 12689–12697.
|
| [26] |
Kuhn H W. The Hungarian method for the assignment problem. Naval Research Logistics Quarterly, 1955, 2: 83–97. DOI: https://doi.org/10.1002/nav.3800020109
|
| [27] |
MMDetection3D Contributors. MMDetection3D: OpenMMLab next-generation platform for general 3D object detection. https://github.com/open-mmlab/mmdetection3d, 2020. Accessed December 1, 2022.
|
| [28] |
Xie E, Yu Z, Zhou D, et al. M2BEV: Multi-camera joint 3D detection and segmentation with unified birds-eye view representation. arXiv: 2204.05088, 2022.
|
| [29] |
Yan Y, Mao Y, Li B. SECOND: Sparsely embedded convolutional detection. Sensors, 2018, 18 (10): 3337. DOI: 10.3390/s18103337
|
| [30] |
Yin T, Zhou X, Krähenbühl P. Center-based 3D object detection and tracking. In: 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Nashville, USA: IEEE, 2021: 11779–11788
|
| [31] |
Wang T, Zhu X, Pang J, et al. Probabilistic and geometric depth: Detecting objects in perspective. In: Proceedings of the 5th Conference on Robot Learning. PMLR, 2022, 164: 1475–1485.
|
| [32] |
Duan K, Bai S, Xie L, et al. CenterNet: keypoint triplets for object detection. In: 2019 IEEE/CVF International Conference on Computer Vision (ICCV). Seoul, Korea: IEEE, 2020: 6568–6577.
|
| [33] |
Nabati R, Qi H. CenterFusion: center-based radar and camera fusion for 3D object detection. In: 2021 IEEE Winter Conference on Applications of Computer Vision (WACV). Waikoloa, HI, USA: IEEE, 2021: 1526–1535.
|
| [34] |
Kim Y, Kim S, Choi J W, et al. CRAFT: Camera-radar 3D object detection with spatio-contextual fusion transformer. arXiv: 2209.06535, 2022.
|
| Method | Modality | NDS↑ | mAP↑ | mATE↓ | mASE↓ | mAOE↓ | mAVE↓ | mAAE↓ | FPS |
| CenterPoint[30] | L | 67.3 | 60.3 | 0.262 | 0.239 | 0.361 | 0.288 | 0.136 | 61 |
| PointPillars[25] | L | 45.3 | 30.5 | 0.517 | 0.290 | 0.500 | 0.316 | 0.368 | 30 |
| FCOS3D[11] | C | 37.2 | 29.5 | 0.806 | 0.268 | 0.511 | 1.315 | 0.170 | 1.7 |
| PGD[31]† | C | 44.8 | 38.6 | 0.626 | 0.245 | 0.451 | 1.509 | 0.127 | 1.4 |
| CenterNet[32] | C | 40.0 | 33.8 | 0.658 | 0.255 | 0.629 | 1.629 | 0.142 | − |
| BEVDet-Tiny[5]† | C | 39.2 | 31.2 | 0.691 | 0.272 | 0.523 | 0.909 | 0.247 | 15.6 |
| CenterFusion[33]† | C+R | 44.9 | 32.6 | 0.631 | 0.261 | 0.516 | 0.614 | 0.115 | − |
| CRAFT[34]† | C+R | 52.3 | 41.1 | 0.467 | 0.268 | 0.456 | 0.519 | 0.114 | 4.1 |
| Ours | C+R | 54.3 | 44.3 | 0.501 | 0.261 | 0.492 | 0.408 | 0.129 | 10.4 |
| Ours-δ | C+R | 57.6 | 48.2 | 0.444 | 0.262 | 0.452 | 0.371 | 0.126 | 10.2 |
| Method | Mod. | Car | Truck | Bus | Trailer | C.V. | Ped. | M.C. | Bicycle | T.C. | Barrier |
| PointPillars[25] | L | 79.9 | 35.7 | 42.8 | 26.1 | 5.5 | 71.7 | 39.4 | 10.6 | 33.4 | 52.0 |
| FCOS3D[11] | C | 47.9 | 23.3 | 31.4 | 11.2 | 5.7 | 41.1 | 30.5 | 30.2 | 55.0 | 45.5 |
| CenterNet[32] | C | 48.4 | 23.1 | 34.0 | 13.1 | 3.5 | 37.7 | 24.9 | 23.4 | 55.0 | 45.6 |
| BEVDet-Tiny[5] | C | 51.2 | 22.3 | 31.3 | 16.0 | 7.2 | 34.5 | 27.3 | 22.5 | 50.0 | 49.8 |
| CenterFusion[33] | C+R | 52.4(+4.0) | 26.5(+3.4) | 36.2(+2.2) | 15.4(+2.3) | 5.5(+2.0) | 38.9(+1.2) | 30.5(+5.6) | 22.9(–0.5) | 56.3(+1.3) | 47.0(+2.6) |
| CRAFT[34] | C+R | 69.6(+21.2) | 37.6(+14.5) | 47.3(+13.3) | 20.1(+7.0) | 10.7(+7.2) | 46.2(+8.5) | 39.5(+14.6) | 31.0(+7.6) | 57.1(+2.1) | 51.1(+5.5) |
| Ours | C+R | 72.1(+20.9) | 43.0(+20.7) | 49.0(+17.7) | 21.6(+5.6) | 14.0(+6.8) | 44.5(+10.0) | 41.1(+13.8) | 42.4(+19.9) | 57.4(+4.0) | 53.9(+4.1) |
| Concat | BF | BSF | #Layers | #Epochs | mAP | NDS | |
| ⅰ | √ | 3 | 12 | 38.4 | 48.7 | ||
| ⅱ | √ | 1 | 12 | 39.0 | 45.0 | ||
| ⅲ | √ | 3 | 12 | 41.3 | 50.0 | ||
| ⅳ | √ | 3 | 12 | 42.6 | 52.4 | ||
| ⅴ | √ | 3 | 20 | 43.3 | 53.4 |
| Class | Modality |  | 20–40 m |  |
| Car | C | 76.2 | 57.3 | 46.4 |
| C+R | 87.4(+11.2) | 76.9(+19.6) | 66.5(+20.1) | |
| Truck | C | 42.6 | 29.4 | 20.3 |
| C+R | 61.1(+18.5) | 49.1(+19.7) | 37.2(+16.9) | |
| Bus | C | 58.6 | 38.8 | 28.8 |
| C+R | 64.2(+5.6) | 54.4(+15.6) | 42.9(+14.1) | |
| Bicycle | C | 40.2 | 22.9 | 19.9 |
| C+R | 49.2(+9) | 36.8(+13.9) | 33.3(+13.4) |
| Modality | Day | Night | Rainy |
| C | 32.2 | 13.2 | 32.8 |
| C+R | 43.3(+11.1) | 23.2(+10.0) | 45.2(+12.4) |