ISSN 0253-2778
CN 34-1054/N
ISSN 0253-2778
CN 34-1054/N
Department of Statistics and Finance, School of Management, University of Science and Technology of China, Hefei 230026, China
Zhishui Hu received his Ph.D. degree in Statistics from the University of Science and Technology of China (USTC) in 2005. He is currently an Associate Professor with the USTC. He is mainly engaged in limit theory. Related research results were published in Annals of Statistics, Journal of Applied Probability, Electronic Journal of Probability, Science China Mathematics, and other academic journals
Liang Dong received his Ph.D. degree in Statistics from the University of Science and Technology of China in 2022. He is currently a lecturer with Nanjing University of Science and Technology. His research mainly focuses on limit theory in random graphs
Liang Dong, E-mail: dongliang@njust.edu.cn
Consider a rooted 















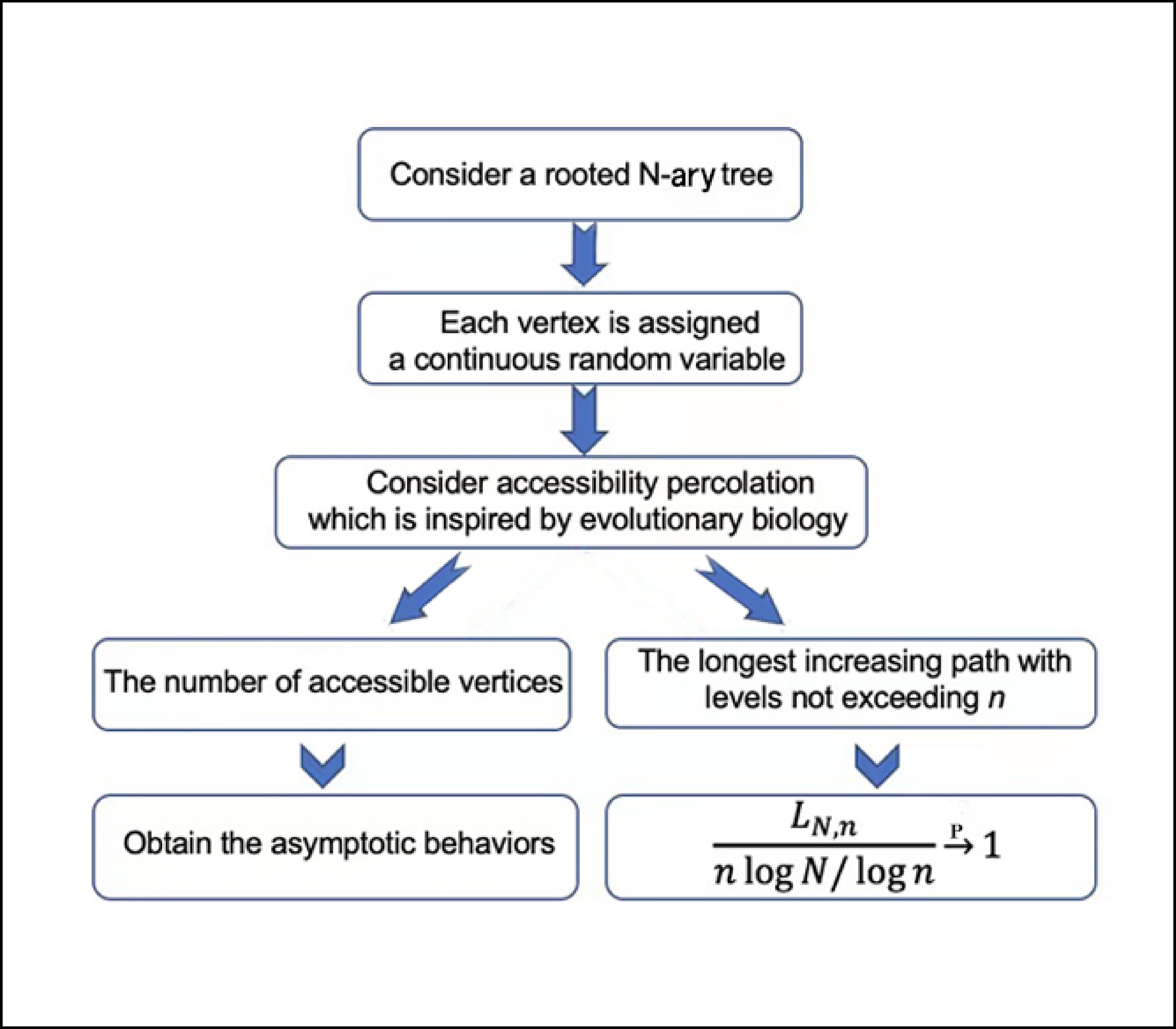
The overall framework of our accessibility percolation on a rooted tree.
Consider a rooted 















For 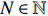
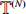
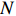
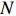
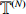
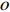
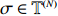
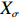

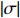
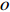

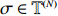
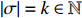
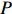
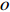

|
\begin{array}{*{20}{l}} o\rightarrow \sigma^{(1)}\rightarrow \sigma^{(2)} \rightarrow \cdots \rightarrow \sigma^{(k-1)}\rightarrow \sigma. \end{array}
|
We say that 
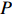
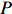
|
\begin{array}{*{20}{l}} X_o< X_{\sigma^{(1)}}< X_{\sigma^{(2)}} < \cdots < X_{\sigma^{(k-1)}}< X_{\sigma}. \end{array}
|
This model is called accessibility percolation by Nowak and Krug[1].
The accessibility percolation model is inspired by evolutionary biology. Each vertex represents one genotype that has an associated fitness value. A particular genotype gives rise to 
The accessibility percolation on 
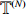
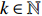
|
\begin{array}{*{20}{l}} Z_{N,\,k}=\displaystyle \sum \limits_{|\sigma|=k} \mathbb{I} (\sigma \; \rm{is accessible}), \end{array}
|
where we sum over all vertices 
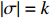
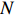
Since we only care about whether the fitness values along a path are in increasing order, as long as the random variables are continuous, changing the precise distribution will not influence the results. Without loss of generality, we assume throughout this work that all the random variables 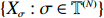
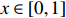
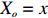
|
\begin{array}{*{20}{l}} \mathbb{P}_x(\cdot)=\mathbb{P}(\cdot \,| X_o=x), \end{array}
|
and denote by 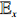
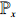
Nowak and Krug[1], Roberts and Zhao[4], Chen[5], and Duque et al.[6] studied the probability 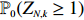
|
\begin{eqnarray} \lim_{N\rightarrow \infty} \mathbb{P}_0(Z_{N,\alpha N}\geqslant 1)=\left\{ \begin{array}{ll} 1, & \rm{if}\; \alpha<{\rm e};\\ 0, & \rm{if}\; \alpha\geqslant {\rm e}. \end{array} \right. \end{eqnarray}
|
(1) |
This implies that there is a phase transition at 
|
\begin{eqnarray} \lim_{N\rightarrow \infty} \mathbb{P}_0(Z_{N,{\rm e} N-\beta \log N}\geqslant 1)=\left\{ \begin{array}{ll} 1, & \rm{if}\; \beta>3/2;\\ 0, & \rm{if}\; \beta<3/2. \end{array} \right. \end{eqnarray}
|
(2) |
He also obtained the asymptotic behaviors of 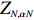
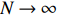
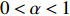
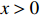
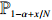
|
\begin{eqnarray} \dfrac{Z_{N,\alpha N}}{m_{N,\alpha}}\stackrel{\rm d}{\longrightarrow} {\rm e}^{-x} Z, \end{eqnarray}
|
(3) |
where 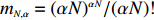

The numbers of increasing paths on other graphs have also been widely studied. Coletti et al.[7] considered infinite spherically symmetric trees, Hegarty and Martinsson[8], Berestycki et al.[9, 10], and Li[11] studied the 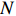
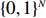
The remainder of this paper is organized as follows. In Section 2, main results are stated. The proofs of Theorems 2.1–2.3 are provided in Section 3. Finally, we present the proof of Theorem 2.4 in Section 4.
We first consider the number of accessible vertices in the first 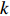
|
\begin{eqnarray} C_{N,\,k}:=\sum_{|\sigma|\leqslant k} \mathbb{I}(\sigma \rm{ is accessible})=\sum_{j=0}^kZ_{N,j}, \end{eqnarray}
|
(4) |
where we sum over all nodes 
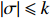
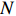
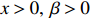
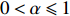

Theorem 2.1. Under 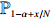
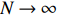
(a) if 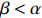
|
\begin{array}{*{20}{l}} {\rm e}^{-\alpha N} C_{N,\,\beta N}\stackrel{\rm p}{\longrightarrow} 0; \end{array}
|
(b) if 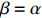
|
\begin{array}{*{20}{l}} {\rm e}^{-\alpha N} C_{N,\,\beta N}\stackrel{\rm d}{\longrightarrow} \dfrac{{\rm e}^{-x} Z}{2}; \end{array}
|
(c) if 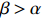
|
\begin{array}{*{20}{l}} {\rm e}^{-\alpha N} C_{N,\,\beta N}\stackrel{\rm d}{\longrightarrow} {\rm e}^{-x} Z. \end{array}
|
We can also study the total number of accessible vertices in the 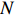
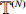
|
\begin{array}{*{20}{l}} C_{N}:=\displaystyle \sum\limits_{\sigma} \mathbb{I}(\sigma \rm{ is accessible}), \end{array}
|
where we sum over all nodes 
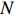
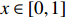
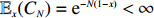
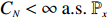
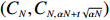
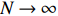
Theorem 2.2. For any 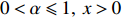
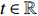

|
\begin{eqnarray} {\rm e}^{-\alpha N}\Big(C_{N}, C_{N,\,\alpha N+t \sqrt{\alpha N}}\Big)\stackrel{\rm d}{\longrightarrow} (1,\varPhi(t)) {\rm e}^{-x} Z,\; \; \; \; N\rightarrow \infty, \end{eqnarray}
|
(5) |
where 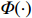
From Theorems 2.1 and 2.2, 

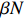

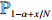




Theorem 2.3. Let 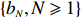


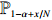
|
\begin{array}{*{20}{l}} \dfrac{C_{N, \alpha N+b_N \sqrt{N}}-C_{N, \alpha N-b_N \sqrt{N}}}{C_N}\stackrel{\rm p}{\longrightarrow} 1, \; \; \; \; N\rightarrow \infty. \end{array}
|
Theorems 2.1–2.3 describe the distribution of the number of accessible vertices from the root 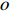
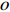
|
\begin{array}{*{20}{l}} M_N:=\max\{|\sigma|: \sigma \rm{ is accessible} \}. \end{array}
|
Noting that 
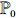
|
\begin{array}{*{20}{l}} \dfrac{M_N-{\rm e}N}{\log N}\stackrel{\rm p}{\longrightarrow}- \dfrac{3}{2},\; \; \; \; N\rightarrow \infty. \end{array}
|
In the related existing results on 


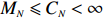
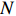


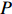

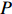
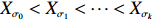
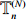

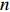
|
\begin{array}{*{20}{l}} L_{N,n}:=\max\{l(P): \; P\; \rm{is an increasing path down} \; \mathbb{T}^{(N)}_n \}. \end{array}
|
Theorem 2.4. Let 
|
\begin{array}{*{20}{l}} \dfrac{L_{N,\,n}}{n \log N /\log n} \stackrel{\rm p}{\longrightarrow} 1,\; \; n\rightarrow \infty. \end{array}
|
In the following Sections 3 and 4, we prove our main results stated above.
Before the proofs, we need the following preliminary lemmas.
Lemma 3.1. Let 

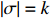

|
\begin{eqnarray} && \mathbb{P}_x(\sigma {\rm \; is \; \; accessible})=\frac{(1-x)^k}{k!}, \end{eqnarray}
|
(6) |
|
\begin{eqnarray} && \mathbb{P}_x (\sigma {\rm \; is \; \; accessible} |X_{\sigma}=y)=\frac{(y-x)^{k-1}}{(k-1)!}. \end{eqnarray}
|
(7) |
Furthermore, let 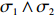
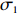



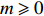


|
\begin{eqnarray} \mathbb{P}_x ({\rm both\; } \sigma_1 {\rm \; and\; } \sigma_2 {\rm \; are \; accessible})=\frac{(1-x)^{m+i+j}(i+j)!}{(m+i+j)!i!j!}. \end{eqnarray}
|
(8) |
Proof. We assume that 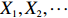
|
\begin{array}{*{20}{l}} \mathbb{P}(X_1<\cdots<X_{k}| x\leqslant X_1 ,\cdots, X_k\leqslant 1)=\dfrac{1}{k!}. \end{array}
|
This, together with 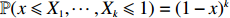
|
\begin{array}{*{20}{l}} \mathbb{P}_x(\sigma~~ \rm{is accessible})=\mathbb{P}(x<X_1<\cdots<X_k\leqslant 1)=\dfrac{(1-x)^k}{k!}. \end{array}
|
Thus Eq. (6) holds. The proof of Eq. (7) is similar and we omit the details here.
We next prove Eq. (8). If 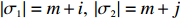
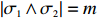


|
\begin{array}{*{20}{l}} &\mathbb{P}_x (\rm{ both } \sigma_1 \rm{ and } \sigma_2 \rm{ are accessible})=&\\ &\mathbb{P} (x<X_1<\cdots<X_{m+i}, \; X_m<X_{m+i+1}<\cdots<X_{m+i+j})=&\\ & \displaystyle \int_x^1 \mathbb{P} (x<X_1<\cdots<X_{m+i},\; X_m<X_{m+i+1}<\cdots<X_{m+i+j}|X_m=y) {\rm d}y=\\ & \dfrac{1}{(m-1)!i!j!}\displaystyle \int_x^1 (y-x)^{m-1} (1-y)^{i+j} {\rm d}y=&\\ & \dfrac{(1-x)^{m+i+j}}{(m-1)!i!j!}\displaystyle \int_0^1 t^{m-1}(1-t)^{i+j}{\rm d}t=&\\ & \dfrac{(1-x)^{m+i+j}(i+j)!}{(m+i+j)!i!j!}, \end{array}
|
where we have used the fact that
|
\begin{array}{*{20}{l}} \displaystyle \int_0^1 t^{m-1}(1-t)^{i+j}{\rm d}t=B(m, i+j+1)=\dfrac{(m-1)!(i+j)!}{(m+i+j)!} \end{array}
|
and 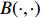
Lemma 3.2. For any 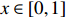
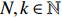
|
\begin{array}{*{20}{l}} \mathbb{E}_x (C_{N,k})=\displaystyle \sum \limits_{n=0}^k \dfrac{N^n}{n!}(1-x)^n,\; \; \; \; \; {\rm Var}_x(C_{N,k})\leqslant (\mathbb{E}_x C_{N,k+1})^2. \end{array}
|
Furthermore, we have 

Proof. Since 

|
\begin{array}{*{20}{l}} \mathbb{E}_x(C_{N,k})=\displaystyle \sum \limits_{|\sigma|\leqslant k} \mathbb{P}_x(\sigma ~~\rm{is accessible}) =\displaystyle \sum\limits_{n=0}^k \dfrac{N^n}{n!}(1-x)^n. \end{array}
|
Similarly,
|
\begin{array}{*{20}{l}} \mathbb{E}_x(C_N)=\displaystyle \sum \limits_{n=0}^{\infty} \dfrac{N^n}{n!}(1-x)^n={\rm e}^{N(1-x)}. \end{array}
|
It is clear that, for any 
|
\begin{split} &\#\{(\sigma_1, \sigma_2): |\sigma_1|=m+i,|\sigma_2|=m+j,|\sigma_1 \wedge \sigma_2|=m\}=\\& \left\{ \begin{array}{ll} (N-1)N^{m+i+j-1}, & i,j>1;\\ N^{m+i+j}, & i=0 \rm{ or } j=0; \end{array} \right. \leqslant N^{m+i+j}. \end{split}
|
(9) |
This, together with Eq. (8), implies that
|
\begin{split} &\mathbb{E}_x(C_{N,k})^2=\\&\displaystyle \sum \limits_{m=0}^k \displaystyle \sum \limits_{i,j=0}^{k-m}\displaystyle \sum \limits_{\sigma_1,\sigma_2} \mathbb{I}(|\sigma_1|=m+i,|\sigma_2|=m+j,\\& |\sigma_1 \wedge \sigma_2|=m) \mathbb{P}_x (\rm{both}\; \sigma_1 \;\rm{and }\; \sigma_2 \;\rm{are accessible})\leqslant \\& \displaystyle \sum \limits_{m=0}^k \displaystyle \sum \limits_{i,j=0}^{k-m} \dfrac{(N(1-x))^{m+i+j}(i+j)!}{(m+i+j)!i!j!}. \end{split}
|
(10) |
By noting that, for any 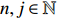
|
\begin{array}{*{20}{l}} \displaystyle \sum\limits_{i=0}^n \dfrac{(i+j)!}{i!j!}= \dfrac{(n+j+1)!}{n!(j+1)!}, \end{array}
|
it follows from (10) that
|
\begin{split} \mathbb{E}_x(C_{N,k})^2\leqslant & \displaystyle \sum \limits_{m+i\leqslant k, m,i\geqslant 0} \displaystyle \sum\limits_{j=0}^k \dfrac{(N(1-x))^{m+i+j}(i+j)!}{(m+i+j)!i!j!}=\\& \displaystyle \sum\limits_{j=0}^k\displaystyle \sum\limits_{n=0}^k \displaystyle \sum\limits_{i=0}^n \dfrac{(N(1-x))^{n+j}(i+j)!}{(n+j)!i!j!}=\\& \displaystyle \sum\limits_{j=0}^k\displaystyle \sum\limits_{n=0}^k \dfrac{(N(1-x))^{n+j}}{n!j!}\dfrac{n+j+1}{j+1}= \\&\displaystyle \sum\limits_{j=0}^k\displaystyle \sum\limits_{n=0}^k \dfrac{(N(1-x))^{n+j}}{n!j!}+ \displaystyle \sum\limits_{j=0}^k\displaystyle \sum\limits_{n=0}^k \dfrac{(N(1-x))^{n+j}n}{n!(j+1)!}\leqslant\\&(\mathbb{E}_x C_{N,k})^2+(\mathbb{E}_x C_{N,k+1})^2, \end{split}
|
(11) |
where we have used
|
\begin{array}{*{20}{l}} \displaystyle \sum\limits_{n=0}^k \displaystyle \sum\limits_{j=0}^k \dfrac{(N(1-x))^{n+j}n}{n!(j+1)!}=\displaystyle \displaystyle \sum\limits_{n=0}^{k-1} \displaystyle \sum\limits_{j=1}^{k+1} \dfrac{(N(1-x))^{n+j}}{n!j!}\leqslant (\mathbb{E}_x C_{N,k+1})^2. \end{array}
|
Therefore 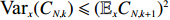
Since 

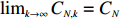
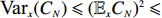
Remark 3.1. For 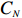
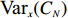
|
\begin{split} &\mathbb{E}_x (C_N)^2=\dfrac{N-1}{N}\displaystyle \sum\limits_{m=0}^{\infty} \displaystyle \sum\limits_{i,j=0}^{\infty} \dfrac{(N(1-x))^{m+i+j}(i+j)!}{(m+i+j)!i!j!}+\\& \dfrac{N+1}{N}\displaystyle \sum\limits_{m=0}^{\infty} \displaystyle \sum\limits_{i=0}^{\infty} \dfrac{(N(1-x))^{m+i}}{(m+i)!}-\displaystyle \sum\limits_{m=0}^{\infty} \dfrac{(N(1-x))^{m}}{m!}=\\&\dfrac{N-1}{N}\displaystyle \sum\limits_{j=0}^{\infty}\displaystyle \sum\limits_{n=0}^{\infty} \dfrac{(N(1-x))^{n+j}}{n!j!}\dfrac{n+j+1}{j+1}+\\&\dfrac{N+1}{N}\displaystyle \displaystyle\sum\limits_{n=0}^{\infty} \dfrac{(N(1-x))^{n}(n+1)}{n!}-{\rm e}^{N(1-x)}=\\&\dfrac{N-1}{N}(2{\rm e}^{2N(1-x)}-{\rm e}^{N(1-x)})+\dfrac{N+1}{N}((N(1-x)+1){\rm e}^{N(1-x)}-{\rm e}^{N(1-x)}=\\&\dfrac{2(N-1)}{N}{\rm e}^{2N(1-x)}+\dfrac{N(N+1)(1-x)+2-N}{N}{\rm e}^{N(1-x)}. \end{split}
|
Thus
|
\begin{array}{*{20}{l}} \rm{Var}_x (C_N)=\dfrac{N-2}{N}{\rm e}^{2N(1-x)}+\dfrac{N(N+1)(1-x)+2-N}{N}{\rm e}^{N(1-x)}. \end{array}
|
Lemma 3.3. For any fixed 

|
\begin{array}{*{20}{l}} \lim\limits_{N\rightarrow \infty} {\rm e}^{-\alpha N}\mathbb{E}_{1-\alpha+x/N}(C_{N,\,\beta N+k}) =\left\{ \begin{array}{ll} 0, & {\rm \; if\; }\beta<\alpha;\\ (1/2){\rm e}^{-x}, & {\rm \; if\; }\beta=\alpha;\\ {\rm e}^{-x}, & {\rm \; if\; }\beta>\alpha. \end{array} \right. \end{array}
|
Proof. For any 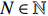
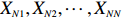
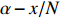


|
\begin{array}{*{20}{l}} P(X_{N1}+\cdots+X_{NN}=n)=\dfrac{{\rm e}^{-(\alpha N-x)}(\alpha N-x)^n}{n!},\; \; \; \; n=0,1,2,\cdots. \end{array}
|
Thus, by Lemma 3.2,
|
\begin{split} \mathbb{E}_{1-\alpha+x/N}(C_{N,\,\beta N+k})= & \displaystyle \sum\limits_{n=0}^{\beta N+k} \dfrac{N^n}{n!}(\alpha-x/N)^n=\\&{\rm e}^{\alpha N-x}\mathbb{P}(X_{N1}+\cdots+X_{NN} \leqslant \beta N+k). \end{split}
|
(12) |
By using the following basic results:
|
\begin{array}{*{20}{l}} \lim\limits_{t\rightarrow 0}\dfrac{{\rm e}^{it}-1-it}{t^2}=-\dfrac{1}{2}, \; \; \; \; \lim\limits_{t\rightarrow 0}{\rm e}^{it}=1, \end{array}
|
we have that, for any 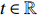
|
\begin{split} &\mathbb{E}\exp\big\{it(X_{N1}+\cdots+X_{NN}-\alpha N)/\sqrt{\alpha N}\big\}=\\&\exp\big\{(\alpha N-x)({\rm e}^{it/\sqrt{\alpha N}}-1)-it\sqrt{\alpha N}\big\}=\\&\exp\big\{\alpha N({\rm e}^{it/\sqrt{\alpha N}}-1-it/\sqrt{\alpha N})-x({\rm e}^{it/\sqrt{\alpha N}}-1)\big\} \rightarrow \\& \exp\{-t^2/2\},\; \; \; \; N\rightarrow \infty. \end{split}
|
Thus
|
\begin{eqnarray} \frac{X_{N1}+\cdots+X_{NN}-\alpha N}{\sqrt{\alpha N}}\stackrel{d}{\longrightarrow} N(0,1),\; \; \; \; N\rightarrow \infty, \end{eqnarray}
|
(13) |
and then
|
\begin{array}{*{20}{l}} \lim\limits_{N\rightarrow \infty}\mathbb{P}(X_{N1}+\cdots+X_{NN}\leqslant \beta N+k)=\left\{ \begin{array}{ll} 0, & \rm{ if }\beta< \alpha;\\ 1/2, & \rm{ if }\beta=\alpha;\\ 1, & \rm{ if }\beta>\alpha. \end{array} \right. \end{array}
|
This, together with (12), proves Lemma 3.3.
For any 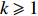
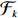

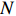
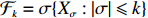
Lemma 3.4. For any 

|
\begin{array}{*{20}{l}} \lim\limits_{k\rightarrow \infty} \lim\limits_{N\rightarrow \infty}\mathbb{P}_{1-\alpha+x/N} \Big({\rm e}^{-\alpha N}\Big|\mathbb{E}(C_{N,\,\beta N} |{\cal{F}}_k)-C_{N,\,\beta N}\Big|>\varepsilon\Big)=0. \end{array}
|
Proof. Let 
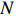

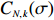
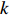

|
\begin{array}{*{20}{l}} C_{N,\,\beta N} =C_{N,\,k}+\displaystyle \sum\limits_{|\sigma|=k} \mathbb{I} (\sigma \rm{ is accessible})C_{N,\, \beta N-k}(\sigma). \end{array}
|
By noting that 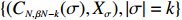
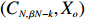
|
\begin{split} \mathbb{E}(C_{N,\,\beta N} |{\cal{F}}_k)=& C_{N,\,k}+\displaystyle \sum\limits_{|\sigma|=k} \mathbb{I} (\sigma ~~\rm{is accessible}) \mathbb{E}_{X_{\sigma}} (C_{N,\, \beta N-k}(\sigma))=\\&C_{N,\,k}+\displaystyle \sum\limits_{|\sigma|=k} \mathbb{I} (\sigma ~~\rm{is accessible}) \mathbb{E}_{X_{\sigma}} (C_{N,\, \beta N-k}), \end{split}
|
and
|
\begin{split} \rm{Var}(C_{N, \,\beta N}|{\cal{F}}_k):=&\mathbb{E}\Big(\Big(\mathbb{E}(C_{N,\,\beta N} |{\cal{F}}_k)-C_{N,\beta N}\Big)^2\Big|{\cal{F}}_k\Big)=\\& \displaystyle \sum\limits_{|\sigma|=k} \mathbb{I} (\sigma ~~\rm{is accessible}) \rm{Var}_{X_{\sigma}} (C_{N, \,\beta N-k}). \end{split}
|
By applying Lemma 3.2, we have that, for any 
|
\begin{array}{*{20}{l}} \rm{Var}_{y} (C_{N, \,\beta N-k})\leqslant \Big(\displaystyle \sum\limits_{n=0}^{\beta N-k+1} \dfrac{N^n}{n!}(1-y)^n\Big)^2\leqslant {\rm e}^{2N(1-y)}. \end{array}
|
Thus,
|
\begin{split} & \mathbb{E}_{1-\alpha+x/N} (\rm{Var}(C_{N,\,\beta N}|{\cal{F}}_k))=\\& N^k \int_{1-\alpha+x/N}^1 \mathbb{P}_{1-\alpha+x/N}(\sigma ~~\rm{is accessible}|X_{\sigma}=y) \rm{Var}_{y} (C_{N,\, \beta N-k}) {\rm d}y\leqslant \\& \dfrac{N^k}{(k-1)!} \int_{1-\alpha+x/N}^1 (y-(1-\alpha+x/N))^{k-1} {\rm e}^{2N(1-y)}{\rm d}y=\\& \dfrac{1}{(k-1)!} \int_{x}^{\alpha N} (z-x)^{k-1} {\rm e}^{2\alpha N-2z}{\rm d}z\leqslant\\& \dfrac{{\rm e}^{2\alpha N-2x}}{(k-1)!} \int_{0}^{\infty} z^{k-1} {\rm e}^{-2z}{\rm d}z=2^{-k}{\rm e}^{2\alpha N-2x}. \end{split}
|
By using Chebyshev’s inequality, we have
|
\begin{split}& \lim_{k\rightarrow \infty} \lim_{N\rightarrow \infty}\,\mathbb{P}_{1-\alpha+x/N} \Big({\rm e}^{-\alpha N}|\mathbb{E}(C_{N,\,\beta N} |{\cal{F}}_k)-C_{N,\beta N}|>\varepsilon\Big)\leqslant\\& \lim_{k\rightarrow \infty} \lim_{N\rightarrow \infty}\dfrac{\mathbb{E}_{1-\alpha+x/N} (\rm{Var}(C_{N,\beta N}|{\cal{F}}_k))}{\varepsilon^2 {\rm e}^{2\alpha N}}=0. \end{split}
|
The proof of Lemma 3.4 is completed.
Lemma 3.5. For any 

|
\begin{split} \lim_{k\rightarrow \infty}\lim_{N\rightarrow \infty}\, & \mathbb{E}_{1-\alpha+x/N} \Big(\exp\{-\lambda {\rm e}^{-\alpha N}\mathbb{E}(C_{N,\,\beta N} |{\cal{F}}_k)\}\Big)=\\& \left\{ \begin{array}{ll} (1+\lambda {\rm e}^{-x})^{-1}, & {\rm if\; }\beta> \alpha;\\ (1+\lambda {\rm e}^{-x}/2)^{-1}, & {\rm if\; }\beta=\alpha;\\ 1, & {\rm if\; }\beta< \alpha. \end{array} \right. \end{split}
|
Proof. By noting that 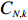

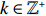
|
\begin{split} &0\leqslant {\rm e}^{-\alpha N}\mathbb{E}_{1-\alpha+x/N} \Big(\mathbb{E}(C_{N,\,\beta N+k} |{\cal{F}}_k)-\mathbb{E}(C_{N,\beta N} |{\cal{F}}_k)\Big)=\\& {\rm e}^{-\alpha N}\mathbb{E}_{1-\alpha+x/N} (C_{N,\,\beta N+k})-{\rm e}^{-\alpha N}\mathbb{E}_{1-\alpha+x/N} (C_{N,\beta N})\rightarrow 0,\; \; \; \; N\rightarrow \infty. \end{split}
|
Thus, to prove Lemma 3.5, it suffices to show that
|
\begin{eqnarray} \lim_{k\rightarrow \infty}\lim_{N\rightarrow \infty}\mathbb{E}_{1-\alpha+x/N} \Big(\exp\{-\lambda {\rm e}^{-\alpha N}\Theta_k\}\Big)=\\ \left\{ \begin{array}{ll} (1+\lambda {\rm e}^{-x})^{-1}, & \rm{if }\; \beta> \alpha;\\ (1+\lambda {\rm e}^{-x}/2)^{-1}, & \rm{if}\; \beta=\alpha;\\ 1, & \rm{if}\; \beta< \alpha, \end{array} \right. \end{eqnarray}
|
(14) |
where
|
\begin{eqnarray} \varTheta_{k}:=\mathbb{E}(C_{N,\beta N+k} |{\cal{F}}_k). \end{eqnarray}
|
(15) |
Write 
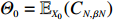
|
\begin{eqnarray} \theta_0(\lambda,x,N)=\exp\{-\lambda {\rm e}^{-\alpha N}\mathbb{E}_{x}(C_{N,\,\beta N})\}. \end{eqnarray}
|
(16) |
Let 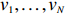
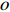

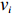

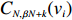


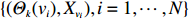

|
\begin{array}{*{20}{l}} \varTheta_{k+1}=1+\displaystyle \sum\limits_{i=1}^N \varTheta_k(v_i)\mathbb{I}(X_{v_i}>X_o), \end{array}
|
we have
|
\begin{split} &\theta_{k+1}(\lambda,x, N)={\rm e}^{-\lambda {\rm e}^{-\alpha N}}\Big(x+\int_x^1 \mathbb{E}_y \Big(\exp\{-\lambda {\rm e}^{-\alpha N}\varTheta_k\}\Big){\rm d}y \Big)^N=\\&{\rm e}^{-\lambda {\rm e}^{-\alpha N}}\Big(1-\int_x^1 (1-\theta_k(\lambda,y,N)) {\rm d}y\Big)^N. \end{split}
|
(17) |
For any 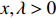
|
\begin{array}{*{20}{l}} Q_0(\lambda, x)=\left\{ \begin{array}{ll} \exp\{-\lambda {\rm e}^{-x}\}, & \rm{if } \; \beta> \alpha;\\ \exp\{-\lambda {\rm e}^{-x}/2\}, & \rm{if } \; \beta=\alpha;\\ 1, & \rm{if } \; \beta< \alpha, \end{array} \right. \end{array}
|
and
|
\begin{array}{*{20}{l}} Q_{k+1}(\lambda, x) = \exp\Big\{-\int_{x}^{\infty} (1-Q_k(\lambda,y)){\rm d}y\Big\},\; \; k\geqslant 0. \end{array}
|
We will show that for any 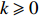

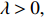
|
\begin{eqnarray} \lim\limits_{N\rightarrow \infty}\theta_k(\lambda,1-\alpha+x/N,N)=Q_k(\lambda,x). \end{eqnarray}
|
(18) |
It follows from Eq. (16) and Lemma 3.3 that Eq. (18) holds true for 
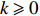
|
\begin{eqnarray} & \theta_{k+1} (\lambda,1-\alpha+x/N,N)=\\ & {\rm e}^{-\lambda {\rm e}^{-\alpha N}}\Big(1-\frac{1}{N}\int_x^{\alpha N} (1- \theta_k(\lambda,1-\alpha+y/N,N)) {\rm d}y\Big)^N. \end{eqnarray}
|
(19) |
Since 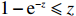
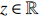
|
\begin{array}{*{20}{l}} 0\leqslant& 1- \theta_k(\lambda,1-\alpha+y/N,N)\leqslant \\& \lambda \mathbb{E}_{1-\alpha+y/N} ({\rm e}^{-\alpha N}\Theta_k)= \mathbb{E}_{1-\alpha+y/N} ({\rm e}^{-\alpha N}C_{N,\,\beta N+k}) \leqslant \\& {\rm e}^{-\alpha N}{\rm e}^{\alpha N-y} \leqslant {\rm e}^{-y}. \end{array}
|
Thus, by the dominated convergence theorem, we obtain
|
\begin{array}{*{20}{l}} \lim\limits_{N\rightarrow \infty}\displaystyle \int_x^{\alpha N} (1- \theta_k(\lambda,1-\alpha+y/N,N)) {\rm d}y =\displaystyle \int_{x}^{\infty} (1-Q_k(\lambda,y)){\rm d}y, \end{array}
|
and then 
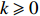
If 


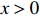
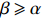
|
\begin{array}{*{20}{l}} \lim\limits_{k\rightarrow \infty} Q_k(\lambda, x)=\left\{ \begin{array}{ll} (1+\lambda {\rm e}^{-x})^{-1}, & \rm{if } \; \beta> \alpha;\\ (1+\lambda {\rm e}^{-x}/2)^{-1}, & \rm{if } \; \beta=\alpha. \end{array} \right. \end{array}
|
Combining this with Eq.(18), we can prove Eq.(14). Thus the proof of Lemma 3.5 is completed.
After these preliminaries, we are now ready to prove Theorems 2.1 and 2.2.
Proof of Theorem 2.1. Here we only prove the case 

|
\begin{split} &\mathbb{P}_{1-\alpha+x/N} \Big({\rm e}^{-\alpha N}C_{N,\,\beta N}\leqslant z\Big) \leqslant \mathbb{P}_{1-\alpha+x/N} \Big({\rm e}^{-\alpha N}\mathbb{E}(C_{N,\,\beta N} |{\cal{F}}_k)\leqslant z+\varepsilon\Big)+\\& \mathbb{P}_{1-\alpha+x/N} \Big({\rm e}^{-\alpha N}|\mathbb{E}(C_{N,\,\beta N} |{\cal{F}}_k)-C_{N,\,\beta N}|>\varepsilon\Big). \end{split}
|
(20) |
By noting that the generating function of 

|
\begin{split} &\lim_{k\rightarrow \infty}\lim_{N\rightarrow \infty}\mathbb{P}_{1-\alpha+x/N} \Big({\rm e}^{-\alpha N}\mathbb{E}(C_{N,\,\beta N} |{\cal{F}}_k)\leqslant z+\varepsilon\Big)=\\&\mathbb{P}({\rm e}^{-x}Z\leqslant z+\varepsilon),\; \; \; \; z\ge 0. \end{split}
|
Thus, by using (20) and Lemma 3.4, we obtain
|
\begin{array}{*{20}{l}} \limsup\limits_{N\rightarrow \infty} \mathbb{P}_{1-\alpha+x/N} \Big({\rm e}^{-\alpha N}C_{N,\,\beta N}\leqslant z\Big)\leqslant \mathbb{P}({\rm e}^{-x}Z\leqslant z+\varepsilon). \end{array}
|
By the arbitrary of 
|
\begin{array}{*{20}{l}} \limsup\limits_{N\rightarrow \infty} \mathbb{P}_{1-\alpha+x/N} \Big({\rm e}^{-\alpha N}C_{N,\,\beta N}\leqslant z\Big)\leqslant \mathbb{P}({\rm e}^{-x}Z\leqslant z). \end{array}
|
Similarly, we can obtain
|
\begin{split} &\mathbb{P}_{1-\alpha+x/N} \Big(C_{N,\,\beta N}/b_N\leqslant z\Big) \geqslant \mathbb{P}_{1-\alpha+x/N} \Big(\mathbb{E}(C_{N,\,\beta N} |{\cal{F}}_k)/b_N\leqslant z-\varepsilon\Big)\nonumber-\\& \mathbb{P}_{1-\alpha+x/N} \Big({\rm e}^{-\alpha N}|\mathbb{E}(C_{N,\,\beta N} |{\cal{F}}_k)-C_{N,\,\beta N}|>\varepsilon\Big), \end{split}
|
and then
|
\begin{array}{*{20}{l}} \liminf\limits_{N\rightarrow \infty} \mathbb{P}_{1-\alpha+x/N} \Big({\rm e}^{-\alpha N}C_{N,\,\beta N}\leqslant z\Big)\geqslant \mathbb{P}({\rm e}^{-x}Z\leqslant z). \end{array}
|
Thus
|
\begin{array}{*{20}{l}} \lim\limits_{N\rightarrow \infty} \mathbb{P}_{1-\alpha+x/N} \Big({\rm e}^{-\alpha N}C_{N,\,\beta N}\leqslant z\Big)= \mathbb{P}({\rm e}^{-x}Z\leqslant z). \end{array}
|
The proof of Theorem 2.1 is completed.
Proof of Theorem 2.2. For any 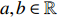
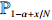
|
\begin{array}{*{20}{l}} {\rm e}^{-\alpha N}\Big(aC_{N}+bC_{N,\, \alpha N+t \sqrt{\alpha N}}\Big)\stackrel{d}{\longrightarrow} (a+b\varPhi(t)) {\rm e}^{-x}Z, \; \; \; \; N\rightarrow \infty. \end{array}
|
This implies (5) by the Cramér-Wold device.
Proof of Theorem 2.3. Note that for any 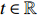

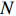
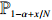
|
\begin{eqnarray} {\rm e}^{-\alpha N}C_{N, \alpha N-b_N \sqrt{N}}\stackrel{p}{\longrightarrow} 0. \end{eqnarray}
|
(21) |
Similarly, for any 

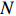
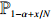
|
\begin{array}{*{20}{l}} {\rm e}^{-\alpha N}(C_N, C_{N,\, \alpha N+b_N \sqrt{N}})\stackrel{d}{\longrightarrow} ({\rm e}^{-x}Z, {\rm e}^{-x}Z). \end{array}
|
Then, under 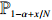
|
\begin{eqnarray} {\rm e}^{-\alpha N}(C_N- C_{N, \,\alpha N+b_N \sqrt{N}})\stackrel{p}{\longrightarrow} 0. \end{eqnarray}
|
(22) |
Therefore, by applying (21), (22), Theorem 2.2 and Slutsky’s theorem, we obtain that under 
|
\begin{split} &\dfrac{C_{N, \alpha N+b_N \sqrt{N}}-C_{N, \alpha N-b_N \sqrt{N}}}{C_N}=\\&1-\dfrac{{\rm e}^{-\alpha N}(C_N- C_{N, \,\alpha N+b_N \sqrt{N}})+{\rm e}^{-\alpha N}C_{N,\, \alpha N-b_N \sqrt{N}}}{{\rm e}^{-\alpha N}C_N}\stackrel{p}{\longrightarrow} 1. \end{split}
|
The proof of Theorem 2.3 is completed.
In this proof, 
Let 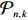

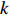


|
\begin{array}{*{20}{l}} T_{n,k}=\displaystyle \sum\limits_{P\in \mathcal{P}_{n,k}} \mathbb{I}\, (P \; \rm{is increasing}). \end{array}
|
By Lemma 3.1, it is clear that
|
\begin{split} \mathbb{E}(T_{n,k})=&\displaystyle \sum\limits_{P\in \mathcal{P}_{n,k}} \mathbb{P}\, (P \; \rm{is increasing})=\\&\displaystyle \sum\limits_{j=0}^{n-k}\displaystyle \sum\limits_{|\sigma_0|=j}\displaystyle \sum\limits_{|\sigma_k|=k+j}\mathbb{P}\, (\sigma_0 \cdots \sigma_k\; \rm{is increasing})=\\&\displaystyle \sum\limits_{j=0}^{n-k}\dfrac{N^j}{(k+1)!}N^k=\dfrac{N^{n+1}-N^k}{(N-1)(k+1)!}. \end{split}
|
Next, we estimate 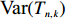
We say that two paths 




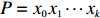
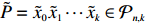


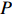



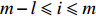
|
\begin{split} &\mathbb{P} (P~~ \rm{and }\; \tilde{P}~~\rm{are increasing})=\int_0^1 \frac{(1-x)^{2k-l}(2k-l-m)!}{(2k-l)!(k-l)!(k-m)!}{\rm d}x=\\&\dfrac{(2k-l-m)!}{(2k-l+1)!(k-l)!(k-m)!}. \end{split}
|
Note that 



|
\begin{split} &\rm{Var}(T_{n,\,k}) =\\& \displaystyle \sum\limits_{P,\, \tilde{P}\in \mathcal{P}_{n,k}} \Big (\mathbb{P} (P~~ \rm{and }\; \tilde{P}~~\rm{are increasing})-\mathbb{P} (P~~ \rm{is increasing})^2\Big) \leqslant\\& {\displaystyle \sum\limits_{P, \; \tilde{P} \in \mathcal{P}_{n,k}\; {\rm{are}}\;{\rm{not}}\; {\rm{vertex}} \text{-}{\rm{disjoint}}}}\mathbb{P} (P~~ \rm{and }\; \tilde{P}~~\rm{are increasing})\leqslant\\& \dfrac{2(N^{n-k+1}-1)N^k}{N-1} \displaystyle \sum\limits_{l=0}^{k}\displaystyle \sum\limits_{m=l}^{k}\dfrac{(2k-l-m)!N^{k-l}}{(2k-l+1)!(k-l)!(k-m)!}=\\& \dfrac{2(N^{n+1}-N^k)}{N-1} \displaystyle \sum\limits_{l=0}^{k}\displaystyle \sum\limits_{m=0}^{ l}\dfrac{(l+m)!N^{l}}{(k+l+1)!l!m!}=\\& \dfrac{2(N^{n+1}-N^k)}{N-1} \displaystyle \sum\limits_{l=0}^{k} \dfrac{(2l+1)!N^l}{(k+l+1)!(l+1)!l!}, \end{split}
|
where in the last equality we have used the equality
|
\begin{array}{*{20}{l}} \displaystyle \sum\limits_{i=0}^n \dfrac{(i+j)!}{i!j!}= \dfrac{(n+j+1)!}{n!(j+1)!},\; \; n, j\in \mathbb{N}. \end{array}
|
Since 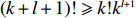
|
\begin{split} \displaystyle \sum\limits_{l=0}^{k}\dfrac{(2l+1)!N^l}{(k+l+1)!(l+1)!l!}\leqslant & \dfrac{1}{Nk!}\sum_{l=0}^{k}{2l+1\choose l+1} (N/k)^{l+1} \leqslant\\& \dfrac{1}{Nk!} (1+N/k)^{2k+1}\leqslant \dfrac{{\rm e}^{3N}}{Nk!}. \end{split}
|
Hence,
|
\begin{eqnarray} \rm{Var}(T_{n,k}) \leqslant \frac{2{\rm e}^{3N} (N^{n+1}-N^k)}{N(N-1)k!}=\frac{2{\rm e}^{3N}}{N} \mathbb{E}(T_{n,k}). \end{eqnarray}
|
(23) |
For any sequence 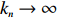
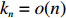
|
\begin{split} \mathbb{E}(T_{n, k_n}) =& \dfrac{N^{n+1}-N^{k_n}}{(N-1)(k_n+1)!}\sim \\&\dfrac{N^{n+1}}{(N-1)\sqrt{2\pi (k_n+1)} (k_n+1)^{k_n+1}{\rm e}^{-(k_n+1)}}=\\&\exp\{n\log N-k_n\log k_n+o(n)\},\; \; \; \; n\rightarrow \infty. \end{split}
|
(24) |
For any 

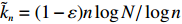
|
\begin{split} \mathbb{P} (L_{N,n}\geqslant (1+\varepsilon)n \log N/\log n) =& \mathbb{P} (T_{n, k_n} \geqslant 1)\leqslant\\& \mathbb{E}(T_{n, k_n}) \rightarrow 0, \; \; \; \; n\rightarrow \infty, \end{split}
|
and furthermore, by Chebyshev’s inequality,
|
\begin{split} \mathbb{P} (L_{N, n}\leqslant (1-\varepsilon)n \log N/\log n) = & \mathbb{P} (T_{n, \tilde{k}_n} =0) \leqslant \\& \frac{ \rm{Var}(T_{n, \tilde{k}_n})}{ (\mathbb{E}(T_{n, \tilde{k}_n}))^2} \leqslant\\& \dfrac{ 2{\rm e}^{3N} }{ N\mathbb{E}(T_{n, \tilde{k}_n})}\rightarrow 0,\; \; \; \; n\rightarrow \infty. \end{split}
|
Then, we obtain Theorem 2.4.
We thank the anonymous referees for the useful suggestions that greatly improved the presentation of this work. This work was supported by the National Natural Science Foundation of China (11671373).
The authors declare that they have no conflict of interest.
The authors declare that they have no conflict of interest.
| [1] |
Nowak S, Krug J. Accessibility percolation on n-trees. Europhysics Letters, 2013, 101 (6): 66004. DOI: 10.1209/0295-5075/101/66004
|
| [2] |
Kingman J F C. A simple model for the balance between selection and mutation. Journal of Applied Probability, 1978, 15 (1): 1–12.
|
| [3] |
Kauffman S, Levin S. Towards a general theory of adaptive walks on rugged landscapes. Journal of Theoretical Biology, 1987, 128 (1): 11–45. DOI: 10.1016/S0022-5193(87)80029-2
|
| [4] |
Roberts M I, Zhao L Z. Increasing paths in regular trees. Electronic Communications in Probability, 2013, 18: 1–10. DOI: 10.1214/ECP.v18-2784
|
| [5] |
Chen X. Increasing paths on N-ary trees. 2014. https://arxiv.org/abs/1403.0843. Accessed March 1, 2022.
|
| [6] |
Duque F, Roldán-Correa A, Valencia L A. Accessibility percolation with crossing valleys on n-ary trees. Journal of Statistical Physics, 2019, 174 (5): 1027–1037. DOI: 10.1007/s10955-019-02223-5
|
| [7] |
Coletti C F, Gava R J, Rodríguez P M. On the existence of accessibility in a tree-indexed percolation model. Physica A: Statistical Mechanics and its Applications, 2018, 492: 382–388. DOI: 10.1016/j.physa.2017.10.019
|
| [8] |
Hegarty P, Martinsson A. On the existence of accessible paths in various models of fitness landscapes. The Annals of Applied Probability, 2014, 24 (4): 1375–1395. DOI: 10.1214/13-AAP949
|
| [9] |
Berestycki J, Brunet E, Shi Z. The number of accessible paths in the hypercube. Bernoulli, 2016, 22 (2): 653–680. DOI: 10.3150/14-BEJ641
|
| [10] |
Berestycki J, Brunet E, Shi Z. Accessibility percolation with backsteps. ALEA Latin American Journal of Probability and Mathematical Statistics, 2017, 14 (1): 45–62. DOI: 10.30757/ALEA.v14-04
|
| [11] |
Li L. Phase transition for accessibility percolation on hypercubes. Journal of Theoretical Probability, 2018, 31 (4): 2072–2111. DOI: 10.1007/s10959-017-0769-x
|
| [12] |
Krug J. Accessibility percolation in random fitness landscapes. In: Probabilistic Structures in Evolution. Berlin: EMS Press, 2021: 1–22
|
| [13] |
Hu Z, Li Z, Feng Q. Accessibility percolation on random rooted labeled trees. Journal of Applied Probability, 2019, 56 (2): 533–545. DOI: 10.1017/jpr.2019.29
|
| 1. | Ren, T., Wu, J. Percolation Problems on N-Ary Trees. Mathematics, 2023, 11(11): 2571. DOI:10.3390/math11112571 |
| [1] |
Nowak S, Krug J. Accessibility percolation on n-trees. Europhysics Letters, 2013, 101 (6): 66004. DOI: 10.1209/0295-5075/101/66004
|
| [2] |
Kingman J F C. A simple model for the balance between selection and mutation. Journal of Applied Probability, 1978, 15 (1): 1–12.
|
| [3] |
Kauffman S, Levin S. Towards a general theory of adaptive walks on rugged landscapes. Journal of Theoretical Biology, 1987, 128 (1): 11–45. DOI: 10.1016/S0022-5193(87)80029-2
|
| [4] |
Roberts M I, Zhao L Z. Increasing paths in regular trees. Electronic Communications in Probability, 2013, 18: 1–10. DOI: 10.1214/ECP.v18-2784
|
| [5] |
Chen X. Increasing paths on N-ary trees. 2014. https://arxiv.org/abs/1403.0843. Accessed March 1, 2022.
|
| [6] |
Duque F, Roldán-Correa A, Valencia L A. Accessibility percolation with crossing valleys on n-ary trees. Journal of Statistical Physics, 2019, 174 (5): 1027–1037. DOI: 10.1007/s10955-019-02223-5
|
| [7] |
Coletti C F, Gava R J, Rodríguez P M. On the existence of accessibility in a tree-indexed percolation model. Physica A: Statistical Mechanics and its Applications, 2018, 492: 382–388. DOI: 10.1016/j.physa.2017.10.019
|
| [8] |
Hegarty P, Martinsson A. On the existence of accessible paths in various models of fitness landscapes. The Annals of Applied Probability, 2014, 24 (4): 1375–1395. DOI: 10.1214/13-AAP949
|
| [9] |
Berestycki J, Brunet E, Shi Z. The number of accessible paths in the hypercube. Bernoulli, 2016, 22 (2): 653–680. DOI: 10.3150/14-BEJ641
|
| [10] |
Berestycki J, Brunet E, Shi Z. Accessibility percolation with backsteps. ALEA Latin American Journal of Probability and Mathematical Statistics, 2017, 14 (1): 45–62. DOI: 10.30757/ALEA.v14-04
|
| [11] |
Li L. Phase transition for accessibility percolation on hypercubes. Journal of Theoretical Probability, 2018, 31 (4): 2072–2111. DOI: 10.1007/s10959-017-0769-x
|
| [12] |
Krug J. Accessibility percolation in random fitness landscapes. In: Probabilistic Structures in Evolution. Berlin: EMS Press, 2021: 1–22
|
| [13] |
Hu Z, Li Z, Feng Q. Accessibility percolation on random rooted labeled trees. Journal of Applied Probability, 2019, 56 (2): 533–545. DOI: 10.1017/jpr.2019.29
|
| 1. | Ren, T., Wu, J. Percolation Problems on N-Ary Trees. Mathematics, 2023, 11(11): 2571. DOI:10.3390/math11112571 |
ISSN 0253-2778
CN 34-1054/N
Copyright © Editorial Office of JUSTC, All Rights Reserved. 皖ICP备05002528号
Supported by: Beijing Renhe Information Technology Co., Ltd. 




 DownLoad:
DownLoad: