ISSN 0253-2778
CN 34-1054/N
Quantum state tomography provides a key tool for validating and fully exploiting quantum resources. However, current protocols of pure-state informationally-complete (PS-IC) measurement settings generally involve various multi-qubit gates or complex quantum algorithms, which are not practical for large systems. In this study, we present an adaptive approach to
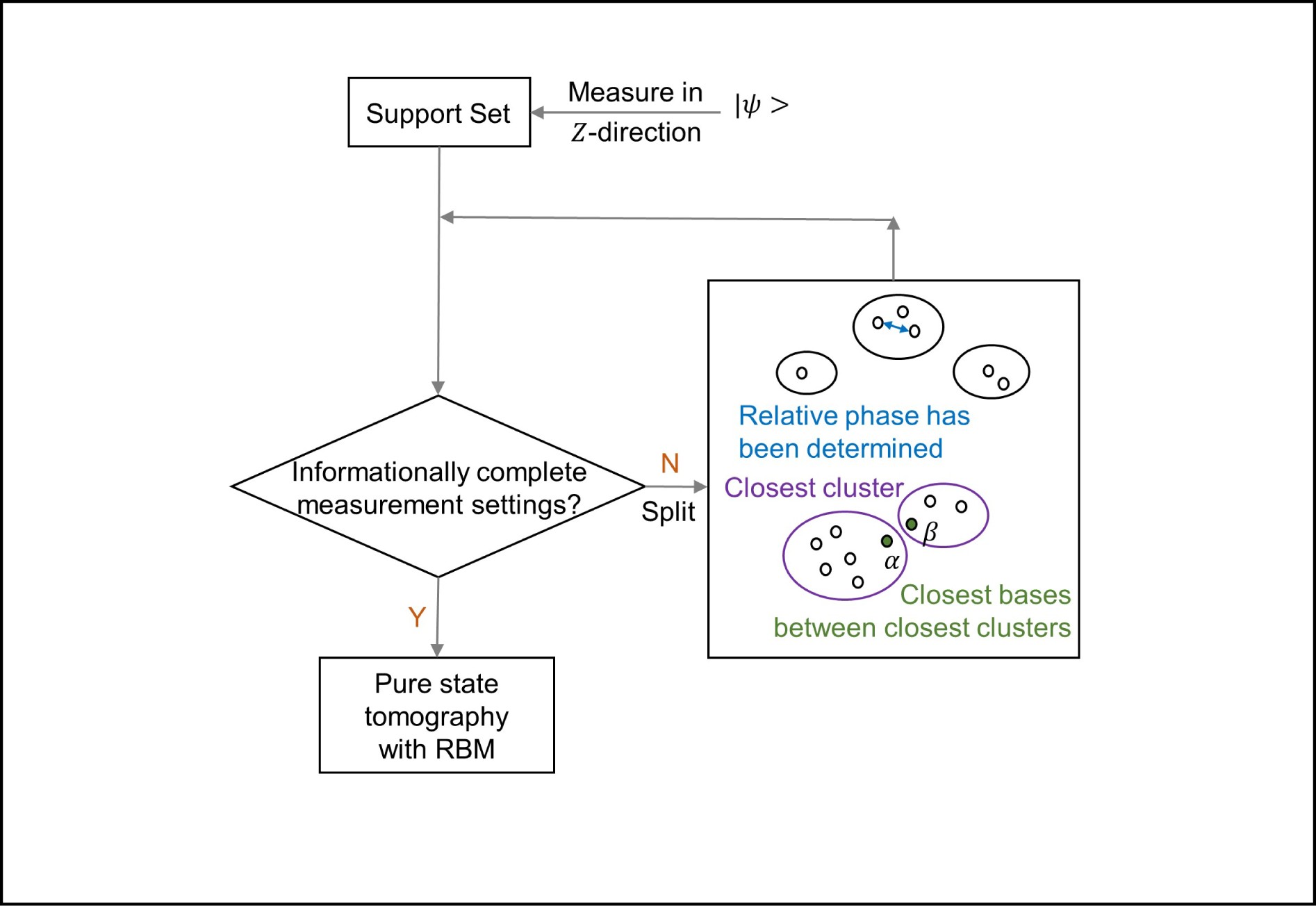
First, projective measurements on each qubit in the Z-direction were implemented to determine the amplitude of each base of the target state. Then, a set of Pauli measurement settings was recursively deduced by the Z-measurement results, which can be used to determine the phase of each base.
Figure
1.
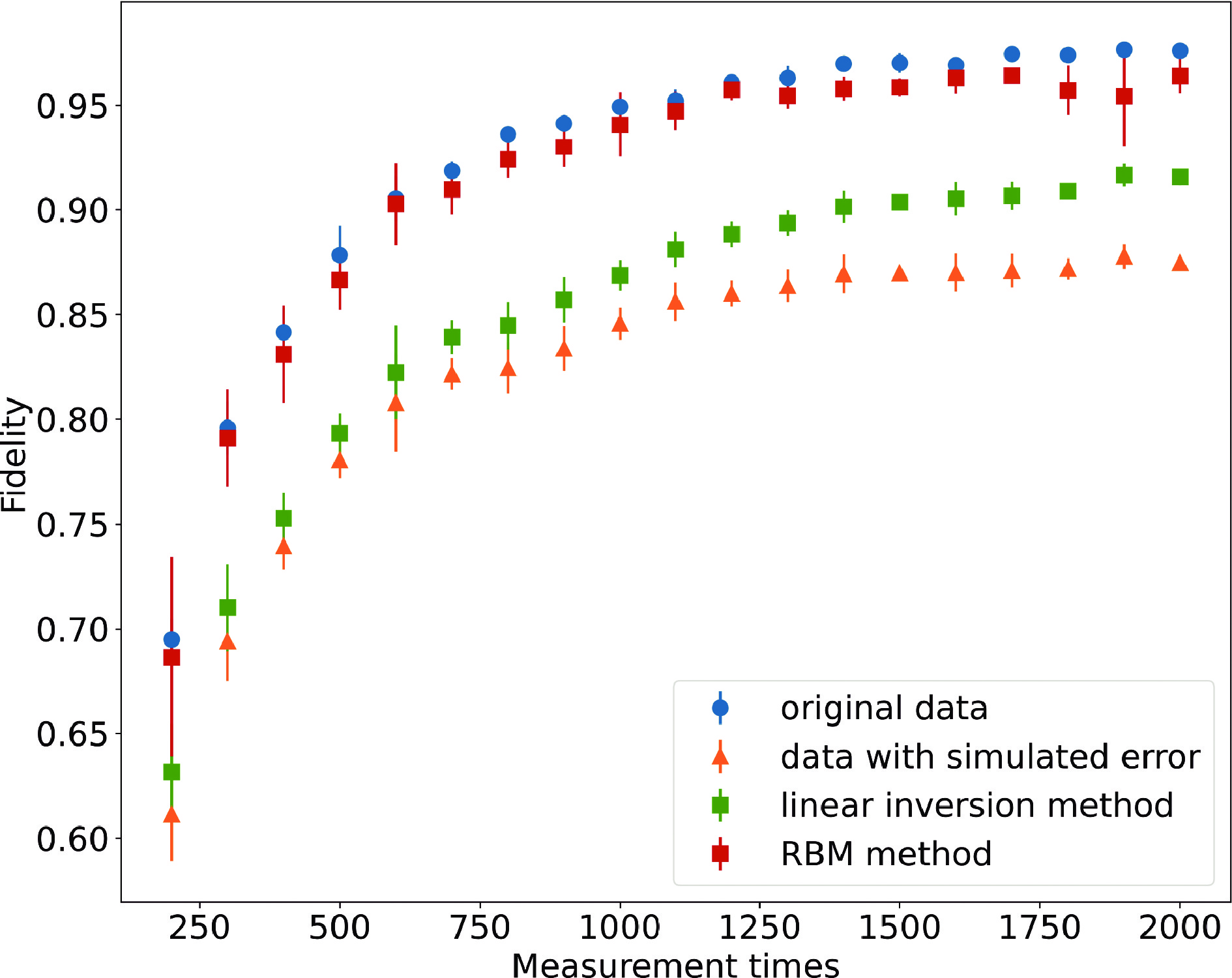
Single-qubit flip error mitigation. The target state is the 10-qubit 1-D chain state, which is introduced in Section 3.3. The results (
| [1] |
Torlai G, Melko R G. Machine-learning quantum states in the NISQ era. Annual Review of Condensed Matter Physics, 2020, 11: 325–344. DOI: 10.1146/annurev-conmatphys-031119-050651
|
| [2] |
Nielsen M A, Chuang I L. Quantum Computation and Quantum Information. Cambridge, UK: Cambridge University Press, 2000.
|
| [3] |
Prugovečki E. Information-theoretical aspects of quantum measurement. International Journal of Theoretical Physics, 1977, 16 (5): 321–331. DOI: 10.1007/BF01807146
|
| [4] |
Busch P. Informationally complete sets of physical quantities. International Journal of Theoretical Physics, 1991, 30: 1217–1227. DOI: 10.1007/BF00671008
|
| [5] |
Heinosaari T, Mazzarella L, Wolf M M. Quantum tomography under prior information. Communications in Mathematical Physics, 2013, 318 (2): 355–374. DOI: 10.1007/s00220-013-1671-8
|
| [6] |
Chen J, Dawkins H, Ji Z, et al. Uniqueness of quantum states compatible with given measurement results. Physical Review A, 2013, 88: 012109. DOI: 10.1103/PhysRevA.88.012109
|
| [7] |
Flammia S T, Silberfarb A, Caves C M. Minimal informationally complete measurements for pure states. Foundations of Physics, 2005, 35 (12): 1985–2006. DOI: 10.1007/s10701-005-8658-z
|
| [8] |
Goyeneche D, Cañas G, Etcheverry S, et al. Five measurement bases determine pure quantum states on any dimension. Physical Review Letters, 2015, 115 (9): 090401. DOI: 10.1103/PhysRevLett.115.090401
|
| [9] |
Finkelstein J. Pure-state informationally complete and “really” complete measurements. Physical Review A, 2004, 70: 052107. DOI: 10.1103/PhysRevA.70.052107
|
| [10] |
Ma X, Jackson T, Zhou H, et al. Pure-state tomography with the expectation value of Pauli operators. Physical Review A, 2016, 93 (3): 032140. DOI: 10.1103/PhysRevA.93.032140
|
| [11] |
Parashar P, Rana S. N-qubit W states are determined by their bipartite marginals. Physical Review A, 2009, 80: 012319. DOI: 10.1103/PhysRevA.80.012319
|
| [12] |
Torlai G, Mazzola G, Carrasquilla J, et al. Neural-network quantum state tomography. Nature Physics, 2018, 14 (5): 447–450. DOI: 10.1038/s41567-018-0048-5
|
| [13] |
Carleo G, Cirac I, Cranmer K, et al. Machine learning and the physical sciences. Reviews of Modern Physics, 2019, 91 (4): 45002. DOI: 10.1103/RevModPhys.91.045002
|
| [14] |
Goodfellow I J, Bengio Y, Courville A. Deep Learning. Cambridge, MA: MIT Press, 2016.
|
| [15] |
Carrasquilla J, Torlai G, Melko R G, et al. Reconstructing quantum states with generative models. Nature Machine Intelligence, 2019, 1: 155–161. DOI: 10.1038/s42256-019-0028-1
|
| [16] |
Torlai G. Augmenting quantum mechanics with artificial intelligence. Waterloo, ON, Canada: University of Waterloo, 2018.
|
| [17] |
Beach M J S, De Vlugt I, Golubeva A, et al. QuCumber: wavefunction reconstruction with neural networks. SciPost Physics, 2019, 7 (1): 009. DOI: 10.21468/SciPostPhys.7.1.009
|
| [18] |
Torlai G, Timar B, van Nieuwenburg E P, et al. Integrating neural networks with a quantum simulator for state reconstruction. Physical Review Letters, 2019, 123 (23): 230504. DOI: 10.1103/PhysRevLett.123.230504
|
| [19] |
Xiao B. Experimental study of quantum entanglement in optical lattices. Hefei: University of Science and Technology of China, 2020.
|
| [20] |
Yang B, Sun H, Huang C J, et al. Cooling and entangling ultracold atoms in optical lattices. Science, 2020, 369 (6503): 550–553. DOI: 10.1126/science.aaz6801
|
| [21] |
Dai H N, Yang B, Reingruber A, et al. Generation and detection of atomic spin entanglement in optical lattices. Nature Physics, 2016, 12 (8): 783–787. DOI: 10.1038/nphys3705
|